el professor
- 4
- 0
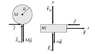
A uniform solid cylinder of mass M and radius R is at rest on a slab of mass m, which in turn rests on a horizontal, frictionless table. If a horizontal force F is applied to the slab, it accelerates and the cylinder rolls without slipping. Find the acceleration of the slab in terms of M, R, and F.
Okay, I'm not usually one to be stumped but this one really has me frustrated. The solution according to the text that I got this problem from says do two free body diagrams (see image), then for the cylinder do sum of forces in the x and the sum of torques about the center of mass and do ƩF on the slab. They then suggest that I relate the acceleration of the cylinder from sum of forces (let's call it ac) to the acceleration of the slab (as) by subtracting the acceleration of the center of mass of the cylinder due to it's rolling, acs (this is acquired from the sum of torques equation done for the cylinder and then using the no slip condition relating angular and tangential acceleration).
I guess I'm okay with the last part -- it is just vector addition (even if I am sceptical about treating a non-inertial reference frame with a that type of tranformation). But there's a big red flag in this explanation (thus this post): the sum of forces in the x on the cylinder is f = m*ac. This is the linear acceleration an outside observer would see the cylinder moving at. I would expect the exact same equation for a block of equal mass resting on the slab. However, my intuition is firmly convinced that the block would not be accelerating at the same rate as the cylinder because the cylinder is rolling back with respect to the slab. In other words, if the slab was invisible, we would see the block pull out ahead of the cylinder.
So, how are we allowed to use the same equation for two obviously different circumstances? Is this the right solution? I brought up the non-inertial reference frame thing earlier because it is the only thing in the solution that rubs me wrong mathematically.
Any help would be appreciated. Thanks!
Okay, I'm not usually one to be stumped but this one really has me frustrated. The solution according to the text that I got this problem from says do two free body diagrams (see image), then for the cylinder do sum of forces in the x and the sum of torques about the center of mass and do ƩF on the slab. They then suggest that I relate the acceleration of the cylinder from sum of forces (let's call it ac) to the acceleration of the slab (as) by subtracting the acceleration of the center of mass of the cylinder due to it's rolling, acs (this is acquired from the sum of torques equation done for the cylinder and then using the no slip condition relating angular and tangential acceleration).
I guess I'm okay with the last part -- it is just vector addition (even if I am sceptical about treating a non-inertial reference frame with a that type of tranformation). But there's a big red flag in this explanation (thus this post): the sum of forces in the x on the cylinder is f = m*ac. This is the linear acceleration an outside observer would see the cylinder moving at. I would expect the exact same equation for a block of equal mass resting on the slab. However, my intuition is firmly convinced that the block would not be accelerating at the same rate as the cylinder because the cylinder is rolling back with respect to the slab. In other words, if the slab was invisible, we would see the block pull out ahead of the cylinder.
So, how are we allowed to use the same equation for two obviously different circumstances? Is this the right solution? I brought up the non-inertial reference frame thing earlier because it is the only thing in the solution that rubs me wrong mathematically.
Any help would be appreciated. Thanks!