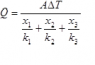How Does Fourier's Law Apply to Heat Flow Through a Composite Wall?

Jay K
Messages
1
Reaction score
0
Using Fourier’s law and an electrical analogy, derive the expression given below for the heat flow, Q, through a flat composite wall of surface area, A, with three layers of thicknesses x1, x2 and x3 and thermal conductivities k1, k2 and k3, and an overall temperature difference ΔT. State any assumptions.
 

Attachments

  • Untitled.png
    Untitled.png
    744 bytes · Views: 435
Physics news on Phys.org
Welcome to PF!

Hi Jay! Welcome to PF! :smile:
Jay K said:
Using Fourier’s law and an electrical analogy …

What do you think the electrical analogy is? :wink:

(and what is Fourier's law?)
 
Thread 'Need help understanding this figure on energy levels'

Thread 'Need help understanding this figure on energy levels'

This figure is from "Introduction to Quantum Mechanics" by Griffiths (3rd edition). It is available to download. It is from page 142. I am hoping the usual people on this site will give me a hand understanding what is going on in the figure. After the equation (4.50) it says "It is customary to introduce the principal quantum number, ##n##, which simply orders the allowed energies, starting with 1 for the ground state. (see the figure)" I still don't understand the figure :( Here is...
View full post »
Thread 'Understanding how to "tack on" the time wiggle factor'

Thread 'Understanding how to "tack on" the time wiggle factor'

The last problem I posted on QM made it into advanced homework help, that is why I am putting it here. I am sorry for any hassle imposed on the moderators by myself. Part (a) is quite easy. We get $$\sigma_1 = 2\lambda, \mathbf{v}_1 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \sigma_2 = \lambda, \mathbf{v}_2 = \begin{pmatrix} 1/\sqrt{2} \\ 1/\sqrt{2} \\ 0 \end{pmatrix} \sigma_3 = -\lambda, \mathbf{v}_3 = \begin{pmatrix} 1/\sqrt{2} \\ -1/\sqrt{2} \\ 0 \end{pmatrix} $$ There are two ways...
View full post »

Similar threads

Thermal conductance of an angular section of a disc
Replies
4
Views
2K
Heat Flow Through a Truncated Cone
Replies
3
Views
4K
Engineering Heat transfer from composite pipe -- Is my answer right?
Replies
1
Views
2K
How is the heat conducted by bar 1 compared to bar 2?
Replies
1
Views
1K
Heat Transfer through multiple walls
Replies
3
Views
2K
I How to measure average thermal conductivity of a metallic material?
Replies
1
Views
2K
Heat Conduction - How long does it take?
Replies
1
Views
3K
A Average temperature in a greenhouse
Replies
2
Views
2K
Fourier's Law of Heat Conduction
Replies
9
Views
4K
A Calculating the heat loss of an open water tank (aquarium)
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top