Gjky424
- 2
- 0
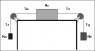
In the figure below, assume that the pulleys are massless and frictionless.
https://www.physicsforums.com/attachment.php?attachmentid=4001&stc=1 23.png
The masses of the blocks are Ma=1.50 kg, Mb=3.00 kg, Mc=5.00 kg, and there is friction between the horizontal plane and Mc, (μk≠0). Mc is observed to travel at a constant velocity.
A. Calculate the coefficient of kinetic friction between Mc and the horizontal surface.
B. Mass Mb is now increased by 0.40 kg. Calculate the magnitude of the acceleration of Mc.
https://www.physicsforums.com/attachment.php?attachmentid=4001&stc=1 23.png
The masses of the blocks are Ma=1.50 kg, Mb=3.00 kg, Mc=5.00 kg, and there is friction between the horizontal plane and Mc, (μk≠0). Mc is observed to travel at a constant velocity.
A. Calculate the coefficient of kinetic friction between Mc and the horizontal surface.
B. Mass Mb is now increased by 0.40 kg. Calculate the magnitude of the acceleration of Mc.