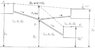
The discussion centers on the flow of water in a system of reservoirs, specifically the equation Q1 = Q2 + Q3, which illustrates how flow from Reservoir A splits into Reservoirs B and C. Participants express confusion about why the equation does not allow for the alternative Q1 + Q2 = Q3, which would imply flow from both A and B to C. The explanation emphasizes that flow direction is determined by pressure differences, with water flowing from higher to lower levels, and that the continuity equation reflects the flow at a junction where water splits. Clarifications are made regarding the necessity of analyzing the entire system rather than individual flows in isolation. Ultimately, the discussion highlights the importance of understanding the underlying principles of fluid dynamics in such scenarios.