How Does the Smaller Block's Slide Affect the Larger Block's Acceleration?

[cupid.callin]

Look at the pic

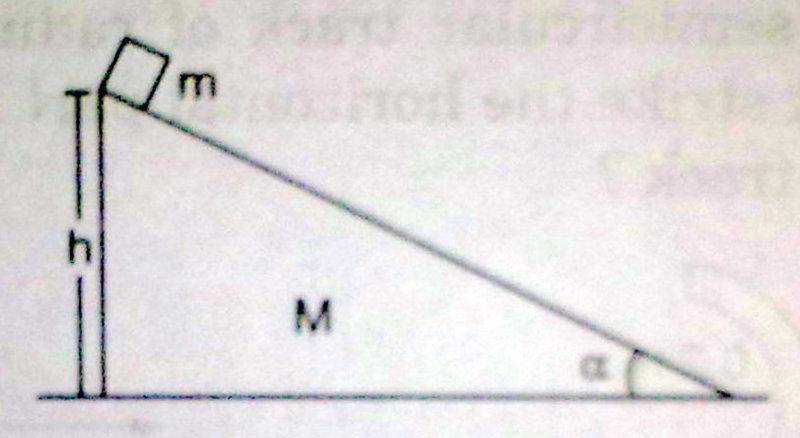
Obviously the smaller block will slide down and the bigger block will accelerate to right ... i want to know that what will be the acceleration of the bigger block ... i have found the answer using that Center of mass has no acceleration. but i want to find out using tradition way ... like F = Ma

What will be the force pushing bigger block towards right?

 

[Doc Al]

What will be the force pushing bigger block towards right?

The block and wedge exert a normal force on each other. That's the force that pushes the wedge. (Looking at your diagram, I'd say that the wedge will move to the left, not the right.)

 

[cupid.callin]

the block exert force of mg(cosα) at the bigger block

so the force in the right direction is mg(cosα)(sinα)

so acceleration is a = mg(cosα)(sinα) / M

but that is wrong

 

[Doc Al]

the block exert force of mg(cosα) at the bigger block

That would be the normal force if the wedge were stationary, but it's not. It accelerates.

 

[ashishsinghal]

the block exert force of mg(cosα) at the bigger block

so the force in the right direction is mg(cosα)(sinα)

so acceleration is a = mg(cosα)(sinα) / M

but that is wrong

That would be true if the block is not accelerating in direction perpendicular to surface of wedge but that is not so because the wedge itself accelerates.

 

[cupid.callin]

I am not getting you guys ...

Am i missing something conceptual?

 

[Doc Al]

On what basis did you conclude that the normal force equals mg(cosα)?

 

[ashishsinghal]

The acceleration of block is along the incline as well as perpendicular to it. Consider this and work on the fbd again

 

[cupid.callin]

Here is my FBD:

and as the cos component of weight gives N so its mgcosα
Is it wrong?

 

[Doc Al]

Here is my FBD:

and as the cos component of weight gives N so its mgcosα
Is it wrong?

Your diagram for the wedge is OK (except that you left out the normal force of the floor on the wedge), but your conclusion that "the cos component of weight gives N" is not correct. N = mgcosα is true for a non-accelerating wedge, since the block would have no acceleration perpendicular to the plane thus the net force in that direction must be zero.

Just call the normal force N. Don't make any assumptions about what it equals.

Your diagram for the block shows the acceleration of the block as being parallel to the plane of the wedge. That's not exactly true, since the wedge accelerates.

Hint: The block is constrained to slide along the wedge. So, in the frame of the wedge, the block accelerates parallel to the surface of the wedge.

(This is a bit tricky, so take it slow.)

 

[SammyS]

Check out this thread: https://www.physicsforums.com/showthread.php?t=478268"

This is a rather nasty problem.

You can't assume that the path of the smaller block is a straight line (in any inertial frame), because the large block has a non-zero acceleration.