How Does This Energy Conservation System Work?

[DeathKnight]

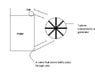
A system is developed as shown in the diagram attached. The ball is initially given a push so that it falls onto a turbine connected to generator which produces electricity. After rotating the turbine the ball fall down a narrow tube with a valve into the water again the ball rises again and is again given a slight push and the whole process is repeated again and again. In this way energy is being "created". The question is: How does this machine obeys the principle of conservation of energy?
Secondly, Why does a raider raiding a bike falls when the bike is stationary but does not fall when its moving? I know that this question has been asked before but I can't find it.
Any help will be appreciated.
(Pardon me for my bad english.)

 

[Tide]

Do you think it is possible to push the ball through the valve and into the water without doing any work?

 

[DeathKnight]

No I dont. In my opinion the KE of the ball will be used to open the valve...

 

[Tide]

And, of course, the ball will have lost some of its energy in turning the turbine.