sparkle123
- 172
- 0
As far as I know, a hyperbola has the equation
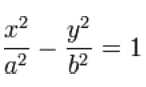
So how does this (below) work?
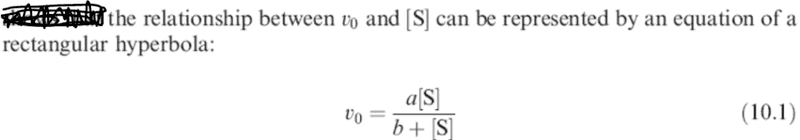
Thanks!
So how does this (below) work?
Thanks!
sparkle123 said:is substrate concentration
vo is the initial rate of an enzyme-catalyzed reaction
Thanks!