~angel~
- 150
- 0
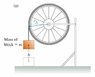
Consider a bicycle wheel that initially is not rotating. A block of mass m is attached to the wheel and is allowed to fall a distance h. Assume that the wheel has a moment of inertia I about its rotation axis.
Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius r_A. Find omega_A, the angular speed of the wheel after the block has fallen a distance h, for this case.
Express omega_A in terms of m, g, h, r_A, and I.
Now consider the case that the string tied to the block is wrapped around a smaller inside axle of the wheel of radius r_B View Figure . Find omega_B, the angular speed of the wheel after the block has fallen a distance h, for this case.
Express omega_B in terms of m, g, h, r_B, and I.
Someone told me that I have incorporate torque into it. I initially thought that you needed to use the conservation of energy, etc. Any help would be great.
Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius r_A. Find omega_A, the angular speed of the wheel after the block has fallen a distance h, for this case.
Express omega_A in terms of m, g, h, r_A, and I.
Now consider the case that the string tied to the block is wrapped around a smaller inside axle of the wheel of radius r_B View Figure . Find omega_B, the angular speed of the wheel after the block has fallen a distance h, for this case.
Express omega_B in terms of m, g, h, r_B, and I.
Someone told me that I have incorporate torque into it. I initially thought that you needed to use the conservation of energy, etc. Any help would be great.