skeer
- 17
- 0
My problem goes :
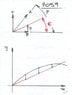
A projectile is fired with initial speed v_0 at an angle of \alpha up a hill slope \beta (\alpha > \beta)
a) How far up the hill will the projectile land.
Attempt to solution:
I understood that this is a problem where I need to find the intersection of the parabola and the line.
the function of the line is y= x tan (\beta)
The parabola is y = [gx^2+2x(v_0)^2cos (\alpha)sin(\alpha) ]/ [ 2(v_0)^2 (\alpha)]
After making them equal to each other I get
x= [2 (v_0)^2 cos (\alpha) sin (\alpha- \Beta) ] / gcos (\beta)
This is almost the answer... but somewhere I made a mistake or I am missing an step. Is my approach correct?
P.S. The answer is d= [2 (v_0)^2 cos (\alpha) sin (\alpha- \Beta) ] / g cos^2 (\beta)
A projectile is fired with initial speed v_0 at an angle of \alpha up a hill slope \beta (\alpha > \beta)
a) How far up the hill will the projectile land.
Attempt to solution:
I understood that this is a problem where I need to find the intersection of the parabola and the line.
the function of the line is y= x tan (\beta)
The parabola is y = [gx^2+2x(v_0)^2cos (\alpha)sin(\alpha) ]/ [ 2(v_0)^2 (\alpha)]
After making them equal to each other I get
x= [2 (v_0)^2 cos (\alpha) sin (\alpha- \Beta) ] / gcos (\beta)
This is almost the answer... but somewhere I made a mistake or I am missing an step. Is my approach correct?
P.S. The answer is d= [2 (v_0)^2 cos (\alpha) sin (\alpha- \Beta) ] / g cos^2 (\beta)
Last edited: