How Fast Can a Ring with Uneven Mass Distribution Roll Without Hopping?

[C-137]

Homework Statement

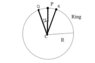
Let there be a ring of mass m and radius r. Let 3 masses be attached to the ring and named as O,P and Q. Mass of O and Q is 2m and mass of p is M. The angle between 2 masses is 15 degrees as shown in the figure.
Find the maximum velocity the ring must roll so that it doesn't hop while rolling i.e. to roll normally (without slipping), not bouncing.

Relevant Equations

Moment of inertia of a ring= mr^2
torque= I*(alpha)

Problem Statement: Let there be a ring of mass m and radius r. Let 3 masses be attached to the ring and named as O,P and Q. Mass of O and Q is 2m and mass of p is M. The angle between 2 masses is 15 degrees as shown in the figure.
Find the maximum velocity the ring must roll so that it doesn't hop while rolling i.e. to roll normally (without slipping), not bouncing.
Relevant Equations: Moment of inertia of a ring= mr^2
torque= I*(alpha)

Tried hard.

 

[BvU]

Hello Cs,

Tried hard.

That's always good. But not good enough at PF. So post your trials to allow us to assist! What's the criterion for hopping off the ground ? At what point in the rotation would that happen ?

 

[C-137]

I guess when
total upward force + normal reaction >= mg

 

[BvU]

What upward force is there except for normal reaction force ?

And what expressions do you have for these ?

 

[haruspex]

I guess when
total upward force + normal reaction >= mg

You are assuming that leaving the ground means the mass centre of the system is accelerating upwards. If I trip while running, I am likely airborne while accelerating downwards,