How Is the Accelerating Force Resolved at the Axle of a Wheel?

[Eugbug]

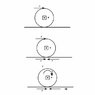
In the diagram attached, a force acts tangentially on the edge of a wheel. To make things easier, the wheel is massless, so moment of inertia doesn't need to be taken into account. However there is a concentrated mass M at the axle(It could be taken as the mass of the axle). Two equal but opposite forces can be introduced at the point of contact with the surface without changing the situation. This then results in a couple whose magnitude is the torque T and also a force F at the surface. The reaction to the force F is the rolling friction force Rf which prevents the wheel from slipping.
How can an accelerating force be resolved at the axle? Do I split the torque T up again into forces? I'm going around in circles thinking about this and it's doing my head in!

 

[Simon Bridge]

I can see why you'd have trouble - torque won't help you because the mass is not distributed.
To use this description, you want to think in terms of levers. If you apply a force twice as far from the fulcrum as the mass, what is the acceleration of the mass?

 

[Eugbug]

I can see why you'd have trouble - torque won't help you because the mass is not distributed.
To use this description, you want to think in terms of levers. If you apply a force twice as far from the fulcrum as the mass, what is the acceleration of the mass?

Well the force at the axle is 2F since the clockwise moment = the anticlockwise moment. So the acceleration is 2F/m. There is no torsion reaction force at the point of contact between the wheel and ground since the "lever" is free to move. So the reaction is simply the inertia of the mass. Inertia can be thought of as a reaction, can't it? (Here I go splitting hairs again!)

 

[Simon Bridge]

In the reference frame of the ground - the point of contact is stationary for an instant. Thus it is a common model to treat it as an instantaneous lever with the fulcrum in the ground.

Same reference frame:
The top point moves twice the instantaneous speed of the center - it got to that speed in the same time.

Consider - the force is being provided by someone pulling on a (very thin) string that is wrapped around the rim of the wheel. If the unrolled length of string increases by length L, the center of the wheel has moved a distance ...

... you can actually conduct an experiment and check if you still doubt this approach.

Note:
Objects are usually considered to have inertia whether they are reacting to something or not.
I think it's a philosophical position to do with the independence of reality from perception... there's a different forum for that sort of discussion though.