How Is the Magnitude of an Electric Field Calculated?

[Linus Pauling]

1.

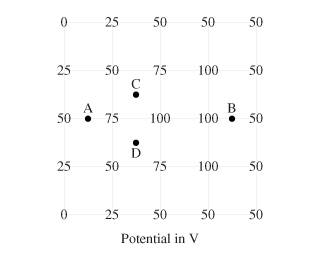
I am then asked to pick the magnitude and direction of E at each point. For all points, I can correctly deduce the direction because the E field points in the direction of decreasing potential. However, what are they doing to calculate the magnitude here? I know the magnitude is 500V/m for A, and I could deduce the correct answers for the rest of the points relative to A.



2. V = U/q = Ed



3. Since I'm not given the charge of a particle at those points, I must need to use some value for d to compute E since V is known for each point. But what d do I use?

 

[ehild]

You get the component of the field strength from the potential difference between the nearest points divided by the distance between them: E=(V1-V2)/d. At A, E = (75-50)/d = 500 V/m.

ehild