BvU said:
You do a moment balance on the cart and I am telling you that you forget a bunch of forces. As Illustrated by the fact that the two forces you do mention point in the same direction, yet an acceleration in that direction is not what you expect.
(ps parallel to the red cross is rather weird, but I understand what you mean -- however, in one paragraph you have the friction parallel and in the next gravity is also parallel...? )
is correct

Humor me and draw a free body diagram of the cart...

Consider force balance and moment balance
jbriggs444 said:
Stop for a moment and re-examine that equation. You are trying to claim that the rate of change of angular momentum of the person is the same as the net torque on the person. Such a claim would be correct.
But what is the rate of change of angular momentum of the person about an inertial axis momentarily positioned between his feet?
Hint: Angular momentum can exist even without rotation.
Edit: I assume that you are intending to analyze in the tangent inertial frame and not the accelerating cart frame. In the cart frame, the relevant effect is accounted for by the fictitious centrifugal force.
haruspex said:
You need to be careful what you mean by that.
If you mean that as a point fixed to the cart then it is accelerating. As jbriggs444 points out, that means you have centrifugal force, and this will have a torque about your reference point.
If you mean it as a point fixed in space, but which happens to be the midpoint of his feet at some instant, then the man has angular velocity wrt that point by virtue of his linear velocity. That angular velocity is changing, and a torque is required to produce that precession.
Ok, so to sum up so far:
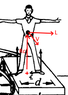
1. if the red-cross is a fixed point in space, then there is angular momentum on the person and the direction of this angular momentum changes but not the magnitude , therefore the derivative of this angular momentum will not be zero , hence , the torque on the person relative to the red-cross the instant the red-cross is exactly between his legs is not zero:
Calculating the angular momentum of the person with respect to the red-cross the instant it is exactly between the legs of the person:
## \vec{L} = \vec{R_c} \times m \vec{V} = R_c \hat{k} \times m \omega R \hat{\theta} = -R_c m \omega R \hat{r}##
## \frac{ \vec{dL} }{dt} = -R_c m \dot{\omega} R \hat{r} -R_c m {\omega}^2 R \hat{\theta} ##
Therefore, at that instant of time :
## -N_1*\frac{d}{2}\hat{k} +N_2*\frac{d}{2}\hat{k} = \frac{ \vec{dL} }{dt} = -R_c m \dot{\omega} R \hat{r} -R_c m {\omega}^2 R \hat{\theta} ##
where:
## R_c ## = distance from red-cross to the center-of-mass of the person , ## \omega ## is the angular velocity of the person with respect to the center of circle about which he is rotating , ## \dot{\omega} ## is the angular acceleration . ## R ## = radius of circle
2. If the red-cross is attached to the cart ( therefore the cross is now a non-inertial system) then , the person is not moving relativly to the cart , therefore the angular momentum of the person is zero , this means the torque is zero and since I find no other new forces when I'm looking at the torque from this non-inertial point ( red-cross attached to moving cart ) , I still get: ##
-N_1*\frac{d}{2} +N_2*\frac{d}{2} = 0 ##
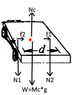
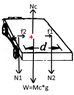
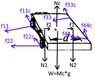
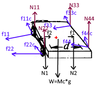
And the force diagram on the cart is:
where ## M_c ## = mass of cart. ## N_c ## = normal force on the cart from the ground . ## f_1 ## and ## f_2 ## are friction forces from the feet of the person.What do you think?