Torque on barbell when angular momentum is not constant

[Soren4]

Homework Statement

[/B]
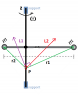
Consider a barbell with two equal masses m that rotates around a vertical axis z not passing through its center with angular velocity \vec{\omega}. The barbell is forced to stay in this position by an appropriate support.
Identify the forces exerting torques on the system and explain what are their effects.

Homework Equations

[/B]
Taking a generic point P on the z axis as pivot point to calculate momenta, the total angular momentum \vec{L}=\vec{L_1}+\vec{L_2} is not parallel to the rotation axis z, thus \vec{L} follows a precession motion and, from the theorem of angular momentum, there must be a torque \vec{\tau} on the system, exterted by external forces: \vec{\tau}=\frac{d \vec{L}}{dt}\neq 0.

The Attempt at a Solution

[/B]
The external forces that have non zero torque are weight (because \vec{r_1} \neq \vec{r_2}) and the reaction of the support. But, since the barbell is forced in this position during the motion, the torque of these two forces should add up to zero (\vec{\tau}=0). On the other hand this is not possible, since \vec{L} is changing over time. How can that be?

 

[haruspex]

The external forces that have non zero torque are weight ... and the reaction of the support. But, since the barbell is forced in this position during the motion, the torque of these two forces should add up to zero . On the other hand this is not possible, since $\vec{L}$ is changing over time. How can that be?

The question is not entirely clear. I assume "the system" is the barbell (rod plus masses), but torque is only meaningful in the context of a reference point - which reference point? It could mean where the barbell meets the axle, or the barbell's mass centre. You seem to have taken it as an arbitrary point on the axle.

 

[Soren4]

Thanks for the answer. Yes the system is only the barbell. Sorry I did not mention that the pivot (or reference point) must be an arbitrary point on the z axis. If P is the point of contact of the barbell with the axis then the angular momentum is totally axial (so it is right that \tau=0) but when P is not in that position? Here is my doubt.
I'm just looking for a qualitative answer (about what forces are acting and the effects). So we can suppose that the point P is on the z axis, at a distance l from the barbell.

 

[TSny]

I'm just looking for a qualitative answer (about what forces are acting and the effects).

You can suppose that the vertical axis is a physical axis mounted in two supports as shown below. The only external forces acting on the system come from these supports unless you also wish to include gravitational forces.

So we can suppose that the point P is on the z axis, at a distance l from the barbell.

Yes.

 

[haruspex]

But, since the barbell is forced in this position during the motion, the torque of these two forces should add up to zero

I was not able to follow your reasoning here. Why should the torques add to zero? Isn't it only necessary that the net torque is orthogonal to the angular momentum?

 

[Soren4]

You can suppose that the vertical axis is a physical axis mounted in two supports as shown below. The only external forces acting on the system come from these supports unless you also wish to include gravitational forces.

Thank you for the drawing! That's the point, gravity is an external force acting on the system too and it exerts torque. On the other hand also supports exert a torque and that's the origin of my doubt, since the total torque on barbell should not be zero, as the angular momentum is changing.

I was not able to follow your reasoning here. Why should the torques add to zero? Isn't it only necessary that the net torque is orthogonal to the angular momentum?

Thanks for the reply! In fact the torques should not add to zero, since \vec{L} is changing and, as you said, the total torque should be orthogonal to the angular momentum vector (which follows a uniform precession motion). Nevertheless if the sum of the torques is not zero then the barbell would change its orientation during the rotation. If it remains in the horizontal position it is because the torque of weight is necessarily balanced by the torque of supports. And that is what bothers me, I cannot understand if the torques balance each other or not. Is my reasoning incorrect?

 

[haruspex]

Thank you for the drawing! That's the point, gravity is an external force acting on the system too and it exerts torque. On the other hand also supports exert a torque and that's the origin of my doubt, since the total torque on barbell should not be zero, as the angular momentum is changing.
Thanks for the reply! In fact the torques should not add to zero, since \vec{L} is changing and, as you said, the total torque should be orthogonal to the angular momentum vector (which follows a uniform precession motion). Nevertheless if the sum of the torques is not zero then the barbell would change its orientation during the rotation. If it remains in the horizontal position it is because the torque of weight is necessarily balanced by the torque of supports. And that is what bothers me, I cannot understand if the torques balance each other or not. Is my reasoning incorrect?

You are told the barbell is forced to stay horizontal by the support. It follows that the support exerts exactly that torque necessary to keep it horizontal.

 

[Soren4]

You are told the barbell is forced to stay horizontal by the support. It follows that the support exerts exactly that torque necessary to keep it horizontal.

Ok, but then \vec{\tau}=0, so how can the angular momentum change over time?

 

[haruspex]

Ok, but then \vec{\tau}=0, so how can the angular momentum change over time?

No, the net torque does not need to be zero to keep the bar horizontal.
Consider just one of the masses, at point A. As you showed, its angular momentum vector about point P is along the line PA', where APA' is a right angle in a vertical plane. Construct a point A" such APA" and A'PA" are also right angles. So we have three mutually orthogonal lines emanating from P. PA" is horizontal.
The forces acting on the mass are all in the plane of APA', so orthogonal to PA". The net torque about P is parallel to PA". This is exactly the same situation as with a leaning gyroscope.

 

[Soren4]

No, the net torque does not need to be zero to keep the bar horizontal.
Consider just one of the masses, at point A. As you showed, its angular momentum vector about point P is along the line PA', where APA' is a right angle in a vertical plane. Construct a point A" such APA" and A'PA" are also right angles. So we have three mutually orthogonal lines emanating from P. PA" is horizontal.
The forces acting on the mass are all in the plane of APA', so orthogonal to PA". The net torque about P is parallel to PA". This is exactly the same situation as with a leaning gyroscope.

Thanks a lot for the answer! I find a bit difficult to visualize what you described but I think I almost got it.
So actually both gravity and support reaction exert torques, but the sum of this two torques is not zero, correct? (Precisely the torque is oriented perpendicular both to \vec{\omega} and the barbell, i.e. coming out of the screen).

 

[haruspex]

Thanks a lot for the answer! I find a bit difficult to visualize what you described but I think I almost got it.
So actually both gravity and support reaction exert torques, but the sum of this two torques is not zero, correct? (Precisely the torque is oriented perpendicular both to \vec{\omega} and the barbell, i.e. coming out of the screen).

Yes.

 

[Soren4]

Ok, thanks so much for your help!
If I may ask one thing, suppose now to take the pivot point P for the caluclation of angular momenta exactly at the intersection between the barbell and the z axis, then the angular momentum is totally axial (i.e. parallel to z axis). This implies that there is no external torque acting on the barbell. Does it mean that the torque exerted on the barbell (by gravity and the support reaction) is zero if calculated with respect to this point P at the intersection between the barbell and the z axis?

 

[haruspex]

Ok, thanks so much for your help!
If I may ask one thing, suppose now to take the pivot point P for the caluclation of angular momenta exactly at the intersection between the barbell and the z axis, then the angular momentum is totally axial (i.e. parallel to z axis). This implies that there is no external torque acting on the barbell. Does it mean that the torque exerted on the barbell (by gravity and the support reaction) is zero if calculated with respect to this point P at the intersection between the barbell and the z axis?

The net torque is zero, yes.