feedmeister
- 22
- 0
Homework Statement
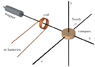
A bar magnet with magnetic dipole moment 0.51 A m^2 lies on the negative x-axis, as shown in the diagram. A compass is located at the origin. Magnetic North is in the negative z direction. Between the bar magnet and the compass is a coil of wire of radius 1.5 cm, connected to batteries not shown in the picture. The distance from the center of the coil to the center of the compass is 9.2 cm. The distance from the center of the bar magnet to the center of the compass is 22.5 cm. A steady current of 0.632 amperes runs through the coil. Conventional current runs clockwise in the coil when viewed from the location of the compass.
How many turns of wire are in the coil?
Homework Equations
B_{loop} = \mu_{0}2\pi R^{2}I/{4\pi}(z^{2}+R^{2})^{3/2}
B_{magnet} = \mu_{0}2\mu/4\pi r^{3}
B_{earth}= 2 E-5 Tesla
\mu_{0}/4\pi = 10^{-7}
I = 0.632 A
\mu = 0.51 A m^{2}
The Attempt at a Solution
I have been trying to do # of turns = (B_{earth} - B_{magnet}) / B_{coil}
and got 100.1271 but it's not the right answer. Can anyone help with what I'm doing wrong?
Attached is a diagram of the problem.
Thanks and regards,