kid
- 5
- 0
Homework Statement
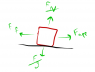
A 15kg crate slides across the floor. The coefficient of kinetic friction between the crate and the floor is 0.28. How much horizontal force is needed to accelerate the crate at 3.0 m/s/s?
Homework Equations
F=ma?
The Attempt at a Solution
F=?
m= 15 kg
u= 0.28
a= 3.0 m/s^2
That's as far as I really got. I'm pretty lost on this one. Thanks for your help.