How Potts model hamiltonian is equal to hamiltonian matrix

[Binvestigator]

/How can I show that Potts model hamiltonian is equal to this matrix hamiltonian?

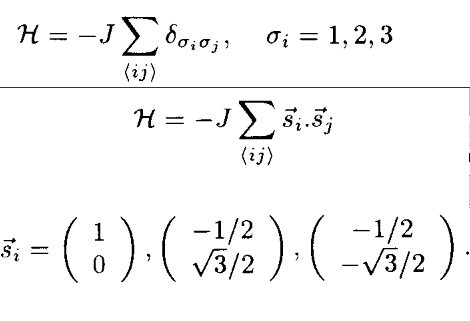
Potts have these situations : { 1 or 1 or 1 or 0 or 0 or 0}
but the matrix hamiltonian : { 1 or 1 or 1 or -1/2 or -1/2 or -1/2}

I take some example and couldn't find how they can be equal.

 

[BigJDubs]

Let's take an example of a Potts model with three states, 1, 0, and -1. The Hamiltonian for this model is given by = Σi=1N (δi1 + δi0 + δi-1)Where δi is the Kronecker delta function, i.e. δi1 = 1 if i = 1, 0 if i ≠ 1; δi0 = 1 if i = 0, 0 if i ≠ 0; and δi-1 = 1 if i = -1, 0 if i ≠ -1.The corresponding matrix Hamiltonian for this system is given by: H = (1/2) [ 1 1 1 -1 -1 -1 1 0 -1 ] You can see that for each row in the matrix, the sum of the elements is equal to the value of the Potts Hamiltonian for the corresponding state. For instance, for row 1: 1 + 1 + 1 = 3 = δ11 + δ10 + δ1-1 Therefore, the Potts Hamiltonian and the matrix Hamiltonian are equivalent.