ambitionz
- 7
- 0
How do I prove that this problem doesn't have a solution?
1. Homework Statement
12. Consider the Leontief system
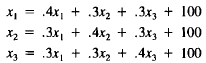
Here the column sums are 1, violating the Leontief input constraint
given in the text. Show that this system cannot have a solution.
Hint: Add the three equations together.
Extra Credit: Try to explain in economic terms why no solution exists.
This is some background info : "An understanding of the economy as consisting of linked sectors goes back to the French economist François Quesnay, and was fully developed by Léon Walras in 1874.[4]However, Wassily Leontief was the first to use a matrix representation of a national (or regional) economy. His model depicts inter-industry relationships within an economy, showing how output from one industrial sector may become an input to another industrial sector. In the inter-industry matrix, column entries typically represent inputs to an industrial sector, while row entries represent outputs from a given sector. This format therefore shows how dependent each sector is on every other sector, both as a customer of outputs from other sectors and as a supplier of inputs. Each column of the input–output matrix shows the monetary value of inputs to each sector and each row represents the value of each sector's outputs"
[/B]
I followed the hint and I added up the three equations.
I got x1 + x2+x3
= x1 + x2+x3 + 300
Since each column represents the demand of each industry, the x1 on the right side of the equation represents the aggregate total of all the demands of an industry; the same goes for x2 and 3 . "x1 + x2+x3 + 300(Consumer demand) " represents the total output of the industries. The "x1 + x2+x3 " represents the total amount of supplies. In order for the system to be in equilibrium the supply must equal the demand. Basically, the left hand side must equal the right hand side. In order for that to happen, x1 + x2+x3 must be 300 less than the amount of the supplies(x1 + x2+x3), consequently, "x1 + x2+x3+300"(the demand) will always be greater than the supply.
Also, does anyone have an idea about the extra credit?
1. Homework Statement
12. Consider the Leontief system
Here the column sums are 1, violating the Leontief input constraint
given in the text. Show that this system cannot have a solution.
Hint: Add the three equations together.
Extra Credit: Try to explain in economic terms why no solution exists.
Homework Equations
This is some background info : "An understanding of the economy as consisting of linked sectors goes back to the French economist François Quesnay, and was fully developed by Léon Walras in 1874.[4]However, Wassily Leontief was the first to use a matrix representation of a national (or regional) economy. His model depicts inter-industry relationships within an economy, showing how output from one industrial sector may become an input to another industrial sector. In the inter-industry matrix, column entries typically represent inputs to an industrial sector, while row entries represent outputs from a given sector. This format therefore shows how dependent each sector is on every other sector, both as a customer of outputs from other sectors and as a supplier of inputs. Each column of the input–output matrix shows the monetary value of inputs to each sector and each row represents the value of each sector's outputs"
The Attempt at a Solution
[/B]
I followed the hint and I added up the three equations.
I got x1 + x2+x3
= x1 + x2+x3 + 300
Since each column represents the demand of each industry, the x1 on the right side of the equation represents the aggregate total of all the demands of an industry; the same goes for x2 and 3 . "x1 + x2+x3 + 300(Consumer demand) " represents the total output of the industries. The "x1 + x2+x3 " represents the total amount of supplies. In order for the system to be in equilibrium the supply must equal the demand. Basically, the left hand side must equal the right hand side. In order for that to happen, x1 + x2+x3 must be 300 less than the amount of the supplies(x1 + x2+x3), consequently, "x1 + x2+x3+300"(the demand) will always be greater than the supply.
Also, does anyone have an idea about the extra credit?
Last edited: