How to Approach Solving a Variable-Mass System with a Falling Drip?

[Michael_0039]

Homework Statement

Falling drip surrounding by water vapor. For t=0, initial mass=M and Uo=0. Prove the following equation...

Relevant Equations

nil

S(t)=

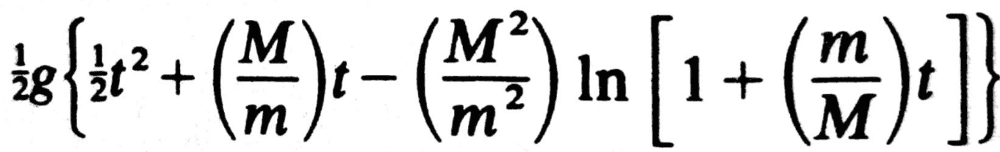
Hi all!

Μy attempt to solve it:

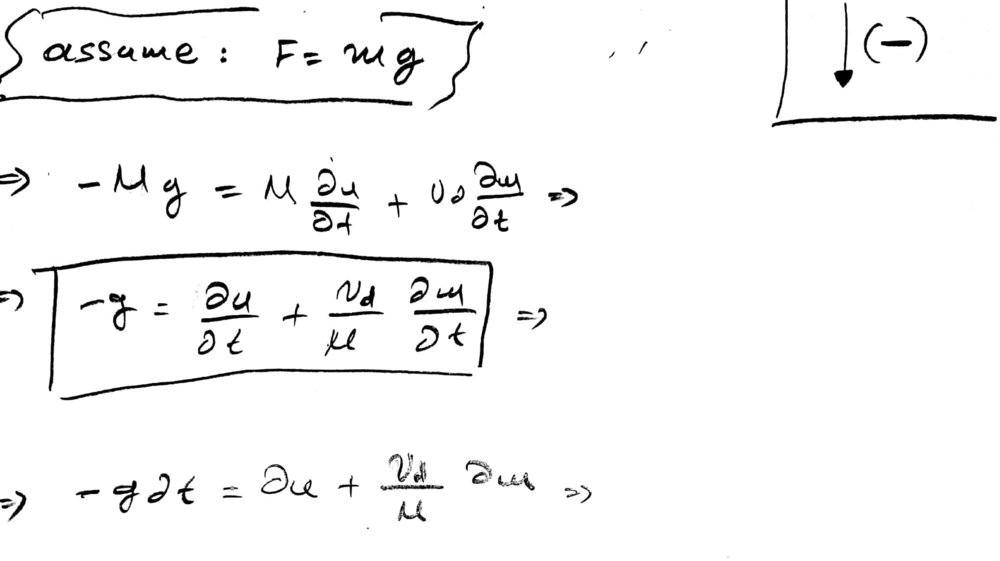
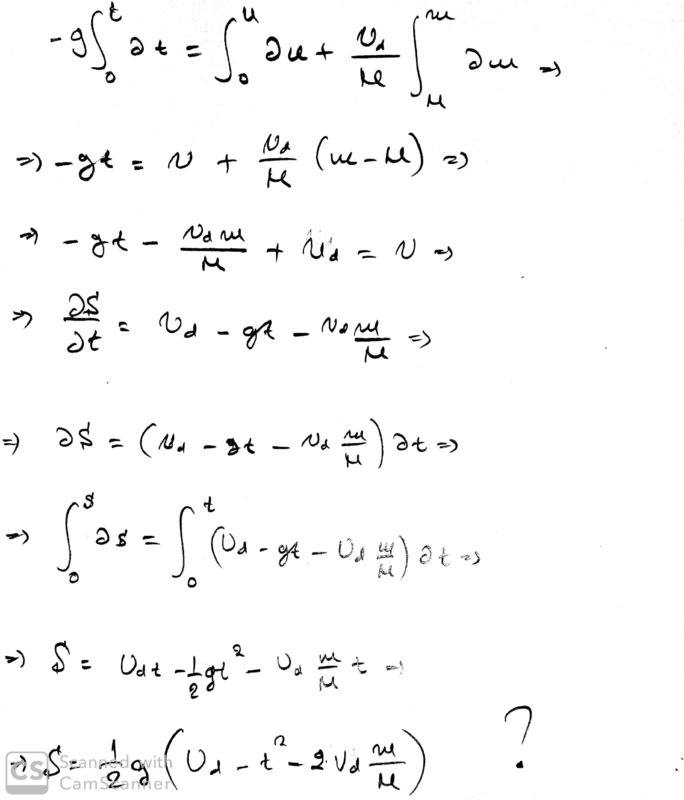I'm stuck here. An opinion ?

Thanks.

 

[Michael_0039]

Edit last line:

S=t (ud-(gt/2)-ud(m/M))

* I dont't know what happened there

 

[Michael_0039]

I made a new attempt to solve it, and reading more for those kind of problems. I made some errors at the previous posts, so this is my attempt now:

I'm on the right track ?

Thanks.

Note:

This is the description:

From: Fundamental University Fhysics Volume 1 (Mechanics), Marcelo Alonso & Edwart J. Finn