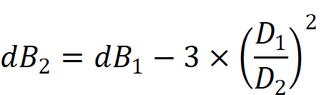How to calculate airplane noise as a function of distance?

[Wes Turner]

TL;DR Summary

How to calculate the reduction in airplane noise as a function of increased distance?

I live close to the (landing) flight path to a major airport. The city has been working with the airport and the FAA to deal with complaints about the noise the jets make as they come in for a landing. I recently attended a meeting where various solutions were discussed, such as changing the flight path or increasing the altitude over residential areas.

I got to wondering how much good that would actually do. I'd like to create a spreadsheet that will calculate the reduction in noise if the plane's altitude is increased from 4,000' to 6,000' or if its overhead path changes from 0.5 miles away from my home to 1.0 miles away.

My foggy memory from my physics classes many years ago tells me that sound decreases as the square of the distance. If the plane is twice as far away, the sound I will hear is 25% (75% less). But I checked a couple of websites and got confusing data. One comfirmed what I thought about the inverse square relationship. Another one said that the sound "pressure" has just an inverse relationship with distance (not the square). I could not figure out what they meant by "pressure".

Finally, one website about decibels said that they are logarithmic. Doubling the distance reduces the sound volume by 6 dB. How much of a reduction is decibels is significant or detectable? And what should the target decibel reading be?

So, how does the sound of an airplane overhead vary with distance? Or is it not that simple?

Thanks

 

[sophiecentaur]

Summary:: How to calculate the reduction in airplane noise as a function of increased distance?

Finally, one website about decibels said that they are logarithmic. Doubling the distance reduces the sound volume by 6 dB.

For a source that's isolated from any other object (i.e. sufficiently high up in the air), the received power will follow the Inverse Square Law. That means the power measured at 2km will be 1/4 the Power at 1km (all other things being equal ) The simplest way to think of the deciBel scale is that if two measured powers have a ratio of 2:1 then that's 3dB. The way logs work means that a ratio of 4:1 will be 6dB
Power Ratio (in dB) = 10 log (Power Ratio) and that works for all numbers you care to put in. dB are worth while getting familiar with because it avoids having loads of zeros in the numbers you want to quote. e.g. a power ratio of 1,000,000 becomes 60dB and a ratio of 0.000001 becomes -60dB
They often describe sound in terms of Sound Pressure Level (SPL) but, because the Power (intensity) is proportional to SPL² so the ratio of SPLs becomes
Ratio in dB is 20log(ratio)
Both are equally valid but hopping from one to the other can give you a headache. You need to get familiar with that stuff because a factor of 2 in the 'dB you quote' can be very important (it's not just twice the loudness but twice the number of zeros!.
There's a lot of information available about the aircraft noise nuisance so, rather than doing your own sums, it's probably best to read a lot (info from both sides). Actual measurements of real cases are much more reliable than calculations because all things are often not equal.

 

[anorlunda]

Airplane noise is also directional. It is not equally loud in all directions.

 

[sophiecentaur]

Local residents near Heathrow are always moaning about takeoff noise. I remember a good few years ago, when planes were much noisier, that they used to takeoff very sharpish to gain height quickly and people (passengers) complained as their stomaches ended up in their mouths. You can't win.

 

[Wes Turner]

For a source that's isolated from any other object (i.e. sufficiently high up in the air), the received power will follow the Inverse Square Law. . . .

Wow! Thanks for that excellent reply. Just what I was looking for.

Based on that, I came up with a little table showing how the sound is reduced as a funtion of the position of the plane. The blue cells are the initial conditions.

Column C is the Y1 values. C7 is Y0. Row 6 is the X1 values. D6 is X0. I chose 4,000' for Y0 because that's the altitude of the planes that pass over our neighborhood. D7 is 100% of whatever the noise is at (X0,Y0), which is at distance Z0 = SQRT(X0^2 + Y0^2).

I did this with percentages. I thought that would be more meaningful to the average user. I suppose I could convert it to dB provided that I had an initial dB value. If I understand dB, the reading in D15, where the sound is down to 25% of the original, would be down 6dB. Is that correct?

The position is determined by this diagram:

Here's the VBA code that does the calculations in Excel:

'================================================================
'                Noise Reduction

' Altitudes are in feet
' Distances are in miles
' This calculation is relative, not absolute,
'   so X0 cannot be set to zero.
'================================================================
Function Noise(pX0 As Double, pY0 As Double, pV0 As Double, _
               pX1 As Double, pY1 As Double) As Double

Const FtPerMi As Double = 5280
Dim R As Double
Dim Z0 As Double, Z1 As Double

Z0 = Sqr((pX0 * FtPerMi) ^ 2 + pY0 ^ 2)
Z1 = Sqr((pX1 * FtPerMi) ^ 2 + pY1 ^ 2)

R = pV0 * (Z0 / Z1) ^

'Noise = Format(R, "0.00")
Noise = R

End Function

 

[Wes Turner]

Airplane noise is also directional. It is not equally loud in all directions.

OK, but if I am comparing the noise level at a fixed position for both the ear and the plane, moving the plane would not affect the calculations significnatly, no?

 

[Wes Turner]

Local residents near Heathrow are always moaning about takeoff noise. I remember a good few years ago, when planes were much noisier, that they used to takeoff very sharpish to gain height quickly and people (passengers) complained as their stomaches ended up in their mouths. You can't win.

Same issues here. Personally, both I and my wife rarely hear the planes and we live near some of the most vocal complainers. I'm just doing this as an exercise in understanding.

 

[anorlunda]

OK, but if I am comparing the noise level at a fixed position for both the ear and the plane, moving the plane would not affect the calculations significnatly, no?

No. At first the plane is coming toward you, then away from you. Probably louder when going away.

 

[Wes Turner]

No. At first the plane is coming toward you, then away from you. Probably louder when going away.

You do know what "fixed position" means, right?

I understand that the sound level varies as the place passes by -- Doppler and all. But at some point in its travels, the sound for someone at a fixed position on the ground is the loudest. That's the only point that matters so that's the point that the calculations are about.

 

[Baluncore]

That's the only point that matters so that's the point that the calculations are about.

Most of the noise from an airplane is radiated behind it, from the jet engine exhausts.

The change in orientation of the aircraft relative to the observer is often more important than the inverse square law.

When an aircraft is approaching you, it sounds quieter than when it is flying away from you.
I expect orientation will make a difference of about 10 dB.
You need to investigate the aircraft noise specifications, and include that in your model.

 

[Wes Turner]

Most of the noise from an airplane is radiated behind it, from the jet engine exhausts.

The change in orientation of the aircraft relative to the observer is often more important than the inverse square law.

When an aircraft is approaching you, it sounds quieter than when it is flying away from you.
I expect orientation will make a difference of about 10 dB.
You need to investigate the aircraft noise specifications, and include that in your model.

OK. I hear you. And I hear the ariplane noise getting louder as it approaches and immediately after it passes overhead. A 10 dB difference from 10° behind to 10° may be reasonable, although isn't 10 dB about a 90% reduction?

But all that will remain more or less the same. The planes will still come from the south and pass over our neighborhood going north. They will just be a little higher and/or a little to the left or right. It seems to me that the inverse square law based just on the distance is a reasonable indication of the actual noise.

Do you disagree?

 

[Baluncore]

Do you disagree?

You are right, but only to the first approximation.

 

[Keith_McClary]

Most of the noise from an airplane is radiated behind it, from the jet engine exhausts.

There was a sports field at the end of a takeoff runway (cheap real estate?). The home team advantage was that visitors could not communicate when planes were taking off. The home team had some workaround.

 

[sophiecentaur]

I suppose I could convert it to dB provided that I had an initial dB value.

The value at the top right (overhead at 4k) value of 100% would be 0dB and all the other values would be negative dB 'cos they're less than 100%.

If I understand dB, the reading in D15, where the sound is down to 25% of the original, would be down 6dB. Is that correct?

Yes - 25% is 0.25. I sympathise if you need to talk to non-technical neighbours.

although isn't 10 dB about a 90% reduction?

Yes - or, better still, a ratio of 0.1. In the case of noise nuisances like this it's fair enough to use percentages but for levels and not for 'reductions'. However, your second quote demonstrates where percentages can be seriously mis-used and mis-understood. People will not / cannot always do the calculation.

Percentages are fine, when used in the context of small price reductions (and small changes in general) but it's possible to look at that "90%" you quote and mis read it as 'down to 90%'. Also, what would 'reduced by 99.9% mean (=reduced TO 0.1%) or 'reduced by 99.95%? Not a problem when we are all in the know about what you mean but it can be used (sometimes deliberately) to mis-lead a reader. Your table is fine and shows the pattern. It shows that height is very relevant near the airport. One small niggle would be that the Table is missing a proper title to say what the sound level value units are (Power or Sound pressure). The values could be very different if your calculation was one way or the other so you should state what they actually are.

I have a similar problem with expressions like 'ten times less'. We all learned fractions in school so why not 'one tenth' - or would '1/12.5' be replaced by 'twelve and a half times less?. Just an old gimmer's whinge - but relevant imo. The OP has avoided this problem.

 

[Baluncore]

Aircraft Noise Models for Assessment of Noise Around Airports – Improvements and Limitations. By Oleksandr Zaporozhets, (Environmental Safety Institute Of The National Aviation University, Kiev, Ukraine)
https://www.icao.int/environmental-...nmentalReports/2016/ENVReport2016_pg50-55.pdf

 

[Wes Turner]

The value at the top right (overhead at 4k) value of 100% would be 0dB and all the other values would be negative dB 'cos they're less than 100%.

I do not understand this. The 100% value in cell D7 is intended to indicate 100% of whatever the noise level is at those coordinates, in this case, 4,000' overhead and 0.0 miles to the left or right. The rest of the percentages are to indicate what the noise level would be relative to those initial conditions.

I replicated the table to do dB calculations. These are the estimated dB readings that correspond to the % readings:

Compare that to these % readings.

And these are the predicted dB readings for an initial reading of 80 dB.

It looks like it is easier to get a meaningful reduction by moving the flight path left or right than by raising the elevation. In many cases, that just means moving the noise to a different neigborhood. In our case, there is water about 1-2 miles away that leads right up to the runways.

 

[Wes Turner]

Aircraft Noise Models for Assessment of Noise Around Airports – Improvements and Limitations. By Oleksandr Zaporozhets, (Environmental Safety Institute Of The National Aviation University, Kiev, Ukraine)
https://www.icao.int/environmental-...nmentalReports/2016/ENVReport2016_pg50-55.pdf

Thank you for that link. Very informative. I'll have to see if I can work any of that into my analysis.

 

[sophiecentaur]

I do not understand this. The 100% value in cell D7 is intended to indicate 100% of whatever the noise level is at those coordinates, in this case, 4,000' overhead and 0.0 miles to the left or right.

I obviously didn't make it clear enough; sorry.

100% is 1.000. Log(1) is zero so 0dB top left. You need too express / convert the percentages as decimals and then do 10log(the decimal value). The dB scale is a scale of Ratios and nothing on your (decimal) table is greater than 1. The dBs will then go from small negative values at the top left region and be more and more negative as you move right and down. (logs of numbers less than one are negative - stick with this, you'll get it.)

 

[Wes Turner]

I obviously didn't make it clear enough; sorry.

100% is 1.000. Log(1) is zero so 0dB top left. You need too express / convert the percentages as decimals and then do 10log(the decimal value). The dB scale is a scale of Ratios and nothing on your (decimal) table is greater than 1. The dBs will then go from small negative values at the top left region and be more and more negative as you move right and down. (logs of numbers less than one are negative - stick with this, you'll get it.)

I think we are talking past each other. My % table is intended to show the relative sound levels for various increases in distance. I am not taking the log of anything in that table. It's just a simple inverse square relationship. Yes, 100% is 1.000, but it's what it is 100% of that matters. It's not the 100% itself.

That equation is:

where D1 & D2 are the line of sight distances from the ear to the planes.

In the dB table, I start with any dB level at D1 and calculate the decibel level at D2. That equation is:

Let me know if I made any errors. (I just fixed a typo.)

 

[berkeman]

In the dB table, I start with any dB level at D1 and calculate the decibel level at D2

Then either start with a realistic dB level or start with a reference level of 0dB. Starting with a 100dB level for a plane 4000 feet overhead makes no sense to me. Do you know how loud that is?

 

[sophiecentaur]

And these are the predicted dB readings for an initial reading of 80 dB.

The dB figures you get for 6000' and 1 mile are 6dB less than the starting values in your tables so the basic calculations are correct, OK? If you actually knew all the characteristics of a particular plane then you could perhaps calculate 'real values' for that table but you'd need to do some actual measurements at various places (hot air balloon?) to calibrate the table.

Starting with the 100dB or 80dB figure is, as @berkeman implies, arbitrary because both those numbers are arbitrary. The thing about deciBels (and, indeed Bels) is that they are Relative numbers. One aeroplane will have a different actual noise level from another when it's at 4k and zero distance. The sort of table you are drawing up is basically intended to show how any plane's noise level will vary, relative to the 'starting point'. So the conventional (and most helpful) thing is to start with a common value of 0dB and the only reason for doing otherwise would be if you actually knew the actual noise values, in which case the dB would be relative to the 'accepted' threshold of hearing level. That's the basis of the dB in acoustics. For electrical signals, the absolute level will often be written relative to a Watt (dBW) or milliwatt (dBmW) or even microWatt (dBμ) but I guess the Sound Engineers got there first and bagged the 'absolute dB'.

 

[Wes Turner]

Then either start with a realistic dB level or start with a reference level of 0dB. Starting with a 100dB level for a plane 4000 feet overhead makes no sense to me. Do you know how loud that is?

You make a good point. Here's the table starting at 0 dB:

That does make it easy to see the reduction.

I chose 100dB just as an example as it made it each for me to confirm the calculations.

I attended a meeting recently where some people were claiming noises close to 100dB at their homes. The airport authorities and the city reps did acknowledge readings as high as 80dB at some of their listening posts, one of which is just a couple of blocks from my home. I have never (or rarely) heard anything that loud. The music from the amphitheater 4 miles away and the stupid kids and their fireworks are much louder.

Anyway, thanks for the suggestion.

 

[Wes Turner]

The dB figures you get for 6000' and 1 mile are 6dB less than the starting values in your tables so the basic calculations are correct, OK?

Good to have that confirmed!

Starting with the 100dB or 80dB figure is, as @berkeman implies, arbitrary because both those numbers are arbitrary.

Yes, for 100dB, but not for 80dB as that was quoted in the city meeting. And I plan to convert this Excel sheet to a Google sheet so anyone can plug in whatever starting value they like.

The sort of table you are drawing up is basically intended to show how any plane's noise level will vary, relative to the 'starting point'.

Exactly.

So the conventional (and most helpful) thing is to start with a common value of 0dB and the only reason for doing otherwise would be if you actually knew the actual noise values, in which case the dB would be relative to the 'accepted' threshold of hearing level. That's the basis of the dB in acoustics.

Agreed. I appreciate the 0dB starting point suggestion. But I do have some actual (claimed) starting points as the city has placed listening posts at several places that have recorded the noise levels. If we then know the target noise level, say 40-60dB, the table will give some idea of how much corrective action will be required.

Again, thanks very much for the help.

 

[sophiecentaur]

100dB for a plane at 4K sounds unlikely to me. Look up typical sound levels in dB. Don’t rely on what people are claiming.

 

[sophiecentaur]

100dB for a plane at 4K sounds unlikely to me

Something that has bugged me for ages is the quoted "100 to 120 dB level for a jet engine sound. I have tried moderately hard to find where the measurement was actually made but can't find it. OTOH, I have read a chain saw noise quoted at a specific distance of 1m. I suspect that the sound level right behind a jet engine could be a tad more than 120dB.

I am not at all impressed that acousticians (who are the sound equivalent of RF transmission experts) are so wooly with their figures. Something that seems to be ignored in discussing sound levels is the fact that, in the presence of the ground, the same amount of sound power is restricted to just a hemisphere so you could have an instant increase of 3dB (6dB at times). Other surrounding objects can easily account for another 3 or more dB. The same will apply to the perception of sound for the air, where the local ground environment can account for similar effects. Do the effects cancel?

Sound nuisance is a very political issue so it may not be in the interests of either individuals or the authorities to have this all nailed down tightly. That would leave nothing to haggle over!

 

[Wes Turner]

It looks like I had an error in my formula for calculating the difference in decibel levels as a function of distance. If I understand it correctly, doubling the distance should subtract 6 dB.

I believe the correct equation is:

Here's a new table with what I believe are the correct values using that equation. Column C has been named D_0 and column D has been named D_1. The @ sign is Excel's new way of selecting the cell from a range that is on the same row or column. The second parameter of the Log function is the base (2).

The first set in blue are all factors of 2, which should be a change of 6 dB. The next set in green are all factors of 4, which should be a change of 12 dB. The next set in light orange are equal, so no change in dB.

The next set are from the city table.

The last line (row 40) is interesting. Sophie commented that my caluclations were correct because the value I showed at 4,000' and 1 mile was -6 dB. Those parameters are for a right triangle with sides of 4000 and 5280. That makes the hypotenuse 7992.396 (=sqrt(4000^2 + 5280^2), which is just close enough to 8000 to return a 6 dB result. If I had shown another decimal place, it would have been 5.99 as in the table above.

That changes the values in my larger table a bit.

Now we see the value in H37 as -5.99 dB. I added the 8000' row (38) so we could see that at 8000' and 0 miles, the distance is exactly double and the table shows -6 dB.

I believe these values are now correct. Please let me know if you see any errors.

Thanks

 

[sophiecentaur]

Where did you get that formula for calculating dB? You may have read someone’s workaround for a particular case but why not use the formula with log base ten?
look at Wiki for all you need to know about deciBels and for the right formula.

I’m not being difficult or elitist here.

 

[Baluncore]

dB₁ = dB₀ - 6.0206 * Log₂( D₀ / D₁ )
Now change the base from 2 to 10.
dB₁ = dB₀ - 20 * Log₁₀( D₀ / D₁ )

 

[sophiecentaur]

dB₁ = dB₀ - 6.0206 * Log₂( D₀ / D₁ )
Now change the base from 2 to 10.
dB₁ = dB₀ - 20 * Log₁₀( D₀ / D₁ )

We all know how to change the bases of logarithms but, apart from in Maths exams, is there any point? There are more steps in the calculation and I still question where the OP found this method and why he chose to use it. Does it get anyone anywhere useful?

I believe the correct equation is:

Here's a new table with what I believe are the correct values

It's a 'correct' version. But why bother? It's only re-arranging the basic formula by using log base 2 instead of log base 10, introducing an error because 6dB is not the exact value and you have to introduce another term in your formula.

The last line (row 40) is interesting. Sophie commented that my caluclations were correct because the value I showed at 4,000' and 1 mile was -6 dB.

I used the percentage table you showed just above it and I read the value in that cell as 25%, which is 6dB lower than the start cell in all your dB tables. Hardly surprising and it checks out.

Your tables would be handy for getting a rough idea of how distance and height is likely to affect what you hear but, the angle changes a lot (reducing as the plane goes further away) so it would be risky to quote those values in a dispute because they are very approximate and could affect your credibility. If more detailed evidence is available then that's what you should quote publicly.

 

[tech99]

I believe that Alexander Graham Bell found that a sound appears half as loud when it is one tenth the power. This is one Bel or 10 decibels. So a 10dB reduction will sound half as loud.
By increasing the distance about three times, the aeroplane will sound half as loud.

 

[sophiecentaur]

I believe that Alexander Graham Bell found that a sound appears half as loud when it is one tenth the power. This is one Bel or 10 decibels. So a 10dB reduction will sound half as loud.
By increasing the distance about three times, the aeroplane will sound half as loud.

But not half as annoying.

 

[Wes Turner]

Where did you get that formula for calculating dB? You may have read someone’s workaround for a particular case but why not use the formula with log base ten?
look at Wiki for all you need to know about deciBels and for the right formula.

The way I get pretty much everything -- by the seat of my pants.

I looked at a bunch of websites, including Wikipedia. I was too lazy to go through all of the math and physics having to do with pressure vs voltage vs who knows what. But the phrase that I read over and over, including here, was that you double the distance and you lose 6 dB. It was pretty easy to come up with my formula from that:

What I didn't realize, and what most of those sites failed to make clear (not Wikipedia) was that it was approximately 6 dB.

I am surprised that someone like you who rails against those who confuse 3 times larger and 3 times as large, one of my minor pet peeves, would not point out that it is only approximately -6 dB.

I have fixed my table. It now looks like this:

I’m not being difficult or elitist here.

Not at all. I have no problem with you pointing out errors in my math or my logic. I appreciate it. And the tone doesn't much matter to me as long as the commentary is correct.

 

[Wes Turner]

dB₁ = dB₀ - 6.0206 * Log₂( D₀ / D₁ )
Now change the base from 2 to 10.
dB₁ = dB₀ - 20 * Log₁₀( D₀ / D₁ )

Thanks for that correction. I have now found that equation on several websites as well. And I just posted my corrected table.

Thanks

 

[Wes Turner]

Your tables would be handy for getting a rough idea of how distance and height is likely to affect what you hear but, the angle changes a lot (reducing as the plane goes further away) so it would be risky to quote those values in a dispute because they are very approximate and could affect your credibility. If more detailed evidence is available then that's what you should quote publicly.

I think this is the key point -- or two points really.

First, I really don't care whether the sound is louder as the aircraft is approaching, directly overhead, or going away. I only care about how loud it is at its loudest point. And unless that is a significant distance from directly overhead so that the line-of-sight distance is significantly greater, it doesn't matter. In addition, the aircraft are on a glide path -- that is, descending. So that will offset at least some of the increase in the distance after it has passed by. And finally, the sound monitors that they have placed in three spots around the city are recording the maximum volume, which is all that the neighbors care about. But unless they are close to your house, the sound you hear would be different.

Second, and this is more important, several comments on the websites and here suggest that the human perception of volume is subjective on several levels, so any instrument reading may not be a perfect measure of what one person or another would perceive.

In short, all I am trying to do is provide a way to measure the relative impact of increasing the elevation of the glide path, moving it farther away, or some combination of both. I argue that whatever the limitations of the numbers in my tables, they can do that job. And in fact, I argue that the percentage table is probably the best at that task. I have heard no complaints about incorrect equations there. It makes it quite clear that moving the glide path 0.75 miles away has the same effect (~50% reduction in volume) as raising the flight path by 1,600', something that the guy from the airport seemed to say was highly unlikely. Furthermore, raising the glide path by the recommended 1,100' and moving it 0.75 miles away will reduce the volume by over 60%.

Do you take issue with any of that?

 

[Wes Turner]

I believe that Alexander Graham Bell found that a sound appears half as loud when it is one tenth the power. This is one Bel or 10 decibels. So a 10dB reduction will sound half as loud.
By increasing the distance about three times, the aeroplane will sound half as loud.

This gets to my second point above to Sophie. Are you saying (or are you saying that Bell said or observed) that while doubling the distance reduces the power to 25%, not only is that not perceived as 25% as loud by people, but it has to get down to 10%, which means increasing the distance by a factor of ~3.16 (10^.5)?