How to Calculate Tension and Acceleration in a Frictionless Pulley System?

Click For Summary

Homework Help Overview

The discussion revolves around calculating tension and acceleration in a frictionless pulley system involving two masses, specifically a 10.0-kg block and a 3.0-kg block. The original poster expresses confusion about how to derive the answers for tension and acceleration despite having some initial calculations related to weights.

Discussion Character

  • Exploratory, Conceptual clarification, Mathematical reasoning

Approaches and Questions Raised

  • Participants suggest identifying the forces acting on each mass and applying Newton's second law to derive equations for tension and acceleration. There is a discussion about the roles of normal force and gravitational force on the masses.

Discussion Status

The discussion is ongoing, with some participants providing guidance on how to approach the problem by focusing on the forces involved. Multiple interpretations of the forces acting on the masses are being explored, particularly regarding the normal force and its cancellation with weight.

Contextual Notes

The original poster has indicated a time constraint due to an upcoming test and has expressed difficulty in progressing from their initial calculations. There is a hint provided regarding the relationship between the distances moved by the two masses.

Miss1nik2
Messages
12
Reaction score
0
Tension question. PLEASE HELP! I have a test tmw!

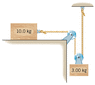
In the drawing, the rope and the pulleys are massless, and there is no friction. Find (a) the tension in the rope and (b) the acceleration of the 10.0-kg block. (Hint: The larger mass moves twice as far as the smaller mass.)I know the answers are 13.7 and 1.37, I just don't know how to get them. PLEASE EXPLAIN IT TO ME!So far I have found that W1 = 98 and W2 = 29.4. And I know the given information M1= 10 and M2= 3. I am completely stuck after that. I have tried in ever way I can think of and I cannot get to the right answer.

Thank you VERY much!
 

Attachments

  • PULLEY.gif
    PULLEY.gif
    3.6 KB · Views: 571
Last edited:
Physics news on Phys.org


Start by indentifying the forces on each mass. Apply Newton's 2nd law to each mass. You'll get two equations, which will allow you to solve for the unknown tension and acceleration.

You might find it helpful to review some of these sample problems: Standard Newton's Laws Problems
 
The forces on each of on each are their weights, and the Normal Force. Which cancel each other out and = 0. Right?
 
Miss1nik2 said:
The forces on each of on each are their weights, and the Normal Force. Which cancel each other out and = 0. Right?
While gravity acts on both masses, only the one on the table will have a normal force. But yes, for that mass the normal force will equal the weight and cancel out.

Don't forget the tension in the rope, which acts on both masses.
 

Similar threads

Newton's Second Law (Pulley Sustem)
  • · Replies 3 ·
Replies
3
Views
2K
Falling mass, additionally accelerated by a rope
  • · Replies 18 ·
Replies
18
Views
2K
How do I calculate the Tension in a rope going over a smooth pulley?
  • · Replies 19 ·
Replies
19
Views
2K
Problem with pulleys - two fixed and one movable
  • · Replies 22 ·
Replies
22
Views
2K
Olympiad dynamics problem with 3 masses and a pulley
  • · Replies 17 ·
Replies
17
Views
3K
Monkey accelerating up and down a rope
  • · Replies 38 ·
2
Replies
38
Views
5K
Tension in a string which connects 3 pulleys
  • · Replies 12 ·
Replies
12
Views
2K
Acceleration of rising mass and tension in cord
  • · Replies 33 ·
2
Replies
33
Views
3K
Angular Acceleration and Linear Acceleration of a Pulley
  • · Replies 4 ·
Replies
4
Views
2K
Acceleration and Tension in Multiple Pulleys
  • · Replies 7 ·
Replies
7
Views
8K