How to calculate the tension in a beam of a bridge?

[Wimpalot]

Homework Statement

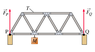
A bridge, constructed of 11 beams of equal length L and negligible mass, supports an object of mass M as shown in the picture.
Assuming that the bridge segments are free to pivot at each intersection point, what is the tension T in the horizontal segment directly above the point where the object is attached (see image)? If you find that the horizontal segment directly above the point where the object is attached is being stretched, indicate this with a positive value for T. If the segment is being compressed, indicate this with a negative value for T.

Homework Equations

t_net = 0 at all points
t = Fr

The Attempt at a Solution

So I worked out that:
F_P = 2/3 Mg
F_Q=1/3 Mg

But after that I have no idea what to do. I am completely lost. I was told to try considering the torques on single points but I don't understand how to do that in this case.

 

[jbriggs444]

The trick in many problems involving torques and rotations is to start by choosing an appropriate axis.

 

[Wimpalot]

The trick in many problems involving torques and rotations is to start by choosing an appropriate axis.

So not just the usual x-y?

 

[jbriggs444]

So not just the usual x-y?

Not the direction of the coordinate axes. The origin of the coordinate system -- the axis of rotation about which you compute torques.

 

[Nidum]

Hint : Look for two self stable substructures .

 

[Wimpalot]

Not the direction of the coordinate axes. The origin of the coordinate system -- the axis of rotation about which you compute torques.

Okay then in that case I am not entirely sure. The point next to the beam?

Hint : Look for two self stable substructures .

Sorry, not sure what you mean/what to do with that information

 

[jbriggs444]

Okay then in that case I am not entirely sure. The point next to the beam?

There are a lot of beams in that truss. Which one did you have in mind?

 

[Wimpalot]

There are a lot of beams in that truss. Which one did you have in mind?

The one I am trying to calculate the tension of. The point on the left?

 

[jbriggs444]

If you write an equation for the torques about that point, you will have contributions from the supporting force from the left pier, the supporting force from the right pier and the downward force from mass M. The tension force T has a line of action that passes through your chosen axis. So it drops out of the equation.

This particular choice of axis does not let you write down a simple equation involving T. It is a poor choice.

Nidum's hint is equally (or perhaps more) important. You want to be computing torques applied to some particular sub-structure. If you think about dividing the truss up into two relevant parts, where might you put the dividing line?

 

[Wimpalot]

If you write an equation for the torques about that point, you will have contributions from the supporting force from the left pier, the supporting force from the right pier and the downward force from mass M. The tension force T has a line of action that passes through your chosen axis. So it drops out of the equation.

This particular choice of axis does not let you write down a simple equation involving T. It is a poor choice.

Nidum's hint is equally (or perhaps more) important. You want to be computing torques applied to some particular sub-structure. If you think about dividing the truss up into two relevant parts, where might you put the dividing line?

I'm not sure then. I have no idea how to do this question. Maybe the left-most triangle?

 

[jbriggs444]

OK.

Maybe the left-most triangle?

OK. Let's say you use the left-most triangle. Now pick an axis of rotation.

 

[Wimpalot]

The point that the mass hangs from?

 

[jbriggs444]

The point that the mass hangs from?

OK. Now what external torques act on that triangle?

 

[Wimpalot]

OK. Now what external torques act on that triangle?

The reaction force F_P and maybe the tension force in the beam T?

 

[jbriggs444]

The reaction force F_P and maybe the tension force in the beam T?

Those are the two of the external forces, yes. To get external torques you would have to multiply by the length of their moment arms, right?

Can you tell us why you ignored the external force from the dangling mass M?

 

[Wimpalot]

Those are the two of the external forces, yes. To get external torques you would have to multiply by the length of their moment arms, right?

Can you tell us why you ignored the external force from the dangling mass M?

And are both moment arms just L? And what about the directions?

Because that way the torque due to the mass is 0

 

[jbriggs444]

And are both moment arms just L? And what about the directions?

Let's start with the torque from the left hand supporting point. Is it clockwise or counter-clockwise? If the left hand supporting force is $F_P$ and the length of the beams is $L$, what is the torque from that left hand supporting force?

Proceed to the torque from the [tension? compression?] T in the horizontal beam. Must it be clockwise or counter-clockwise? Does that mean that it is tension? Or compression? How large is the torque? Be careful. It's not all right angles for this one.

Because that way the torque due to the mass is 0

Good. That is why choosing that point for the axis of rotation was wise. Neither the weight of the dangling mass M nor any forces from the beams to the right contribute to the torque around that axis.

 

[Wimpalot]

Clockwise so negative and thus equal to F_P*L
Is it equal to the tension and L*sin(60)? I am not sure. It would have to be tension right to counteract the other torque?

 

[jbriggs444]

Clockwise so negative and thus equal to F_P*L

Yes, the torque from the left hand pier is clockwise and its magnitude is F_P*L. Yes, if you adopt the convention that clockwise is negative, that means that it is negative.

Is it equal to the tension and L*sin(60)?

You do not sound very sure. But yes, the moment arm is given by L*sin(60).

It would have to be tension right to counteract the other torque?

Let's go slowly. We can do this with mathematics (positives and negatives). Or we can do it with physical intuition (balancing clockwise and counter-clockwise torques).

Let's try the mathematical way. The triangle is both massless and is continuously at rest. The sum of the torques on it must be equal to _____?

 

[Wimpalot]

Zero

 

[jbriggs444]

Zero

So does that give you an equation to solve?

 

[Wimpalot]

So does that give you an equation to solve?

0 = -F_P*L + T*L*sin(60)
Which implies:

T = F_P*L/(L*sin(60))

 

[jbriggs444]

0 = -F_P*L + T*L*sin(60)
Which implies:

T = F_P*L/(L*sin(60))

So the torque due to T is positive or negative?
And the force due to T must therefore be in which direction?

 

[Wimpalot]

So the torque due to T is positive or negative?
And the force due to T must therefore be in which direction?

Negative? Which implies compression.

 

[jbriggs444]

Negative? Which implies compression.

What's negative?
Unless you identify what you are talking about and what sign convention you are using, "positive" and "negative" are just meaningless noises.

 

[Wimpalot]

What's negative?
Unless you identify what you are talking about and what sign convention you are using, "positive" and "negative" are just meaningless noises.

Sorry the torque due to T is negative.
I broke the space key on my keyboard so I am being a bit lazy with words.

 

[jbriggs444]

Sorry the torque due to T is negative.
I broke the space key on my keyboard so I am being a bit lazy with words.

So you add a negative to a negative and get zero?

[Back in #18, you said that the torque due to F_P was negative. Now you say that the torque due to T is also negative]

 

[Wimpalot]

So you add a negative to a negative and get zero?

[Back in #18, you said that the torque due to F_P was negative. Now you say that the torque due to T is also negative]

Sorry I got mixed up the torque due to the tension should be positive.

 

[jbriggs444]

Sorry I got mixed up the torque due to the tension should be positive.

Ok. And since your convention is that positive is counter-clockwise, we are talking about compression. If T is the "tension" in that beam then T must be negative.

So, can you now solve for T?

 

[Wimpalot]

Ok. And since your convention is that positive is counter-clockwise, we are talking about compression. If T is the "tension" in that beam than T must be negative.

So, can you now solve for T?

Yeah just T = -FP*L/(L*sin(60)) which is correct according the site.

Thank you very much for all the help I really feel like I understand this now and can apply it all in the future so thank you very much.