- #1
Whazupp
- 8
- 0
- TL;DR Summary
- In bathroom remodelling, curved surfaces are made by serrating polystyrene (XPS) board and bending it. But there are no instructions on how to make the cuts to get the board to curve spherically. Is it possible somehow?
Example of normal application:

What i'd like to achieve:

More information:
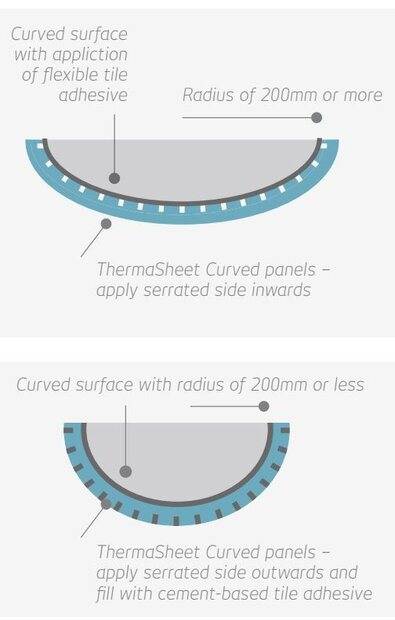
Wedi board serration either straight or angled depending on radii wanted.
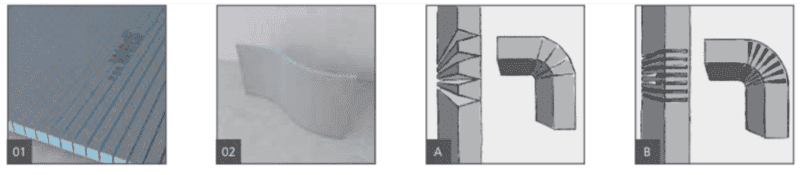
It's also possible to serrate outwards to achieve radii less than 200mm (example from ThermaSheet)
Any ideas on how to do this?
What i'd like to achieve:
More information:
Wedi board serration either straight or angled depending on radii wanted.
It's also possible to serrate outwards to achieve radii less than 200mm (example from ThermaSheet)
Any ideas on how to do this?