How to find the volume of a hemisphere on top of a cone

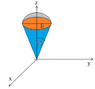
[Another]

Volume of hemi-sphere = ∫ ∫ ∫ r² sinθ dr dθ dφ

i thing (r < r < (r + R)cosθ ) ( 0 < θ < 60 = π/6) and ( 0 < φ < 2π)

integral = 2π ∫ ⅓r³ sin θ dθ

= 2π ∫ ⅓ [((r+R)cosθ)³ - r³] sin θ dθ

i don't know how to find volume of hemi-spere

 

[fresh_42]

Please do not open more than one thread with the same topic, especially if the two are both ambiguous: with or without cone, what is $r$ needed for and what is $a$ in your other thread. Furthermore, do not delete the homework template, use it! It makes reading a lot easier and if you delete it, it can be viewed as disrespectful to those who are willing to answer.

I closed the other one.

 

[Another]

Please do not open more than one thread with the same topic, especially if the two are both ambiguous: with or without cone, what is $r$ needed for and what is $a$ in your other thread. Furthermore, do not delete the homework template, use it! It makes reading a lot easier and if you delete it, it can be viewed as disrespectful to those who are willing to answer.

I closed the other one.

I'm sorryi have problem about find volume of hemisphere on cone using triple integral. (spherical coordinates)
I do not know the true extent of r (From 0 to ?)

 

[fresh_42]

Beside what I've written in the other thread, with the mistakes mentioned and referring to the hemisphere without the cone involved, the final radius is $R$. You had it almost all, beside that $\cos \frac{\pi}{2}=0$ and $\cos 0 = 1$ you only had to solve $\int_0^R r^2dr$ plus eventually the volume of the cone. I assume that it is a full hemisphere above the cone and the angle of $30°$ refers to the cone alone.

 

[LCKurtz]

Too bad the OP has apparently abandoned this thread. It is a half way interesting problem if done directly in untranslated spherical coordinates.