- #1
Karl Karlsson
- 104
- 12
- Homework Statement
- The Nyquist curve for a fifth order system with transfer function G(s) is given in the attached photo. Here we have plotted G (iω) for both positive and negative frequencies ω. The transfer function G(s) has no poles or zeros strictly in the right hemisphere
- Relevant Equations
- None
The Nyquist curve for a fifth order system with transfer function G(s) is given in the attached photo. Here we have plotted G(iω) for both positive and negative frequencies ω. The transfer function G(s) has no poles or zeros strictly on the right side of the imaginary axis
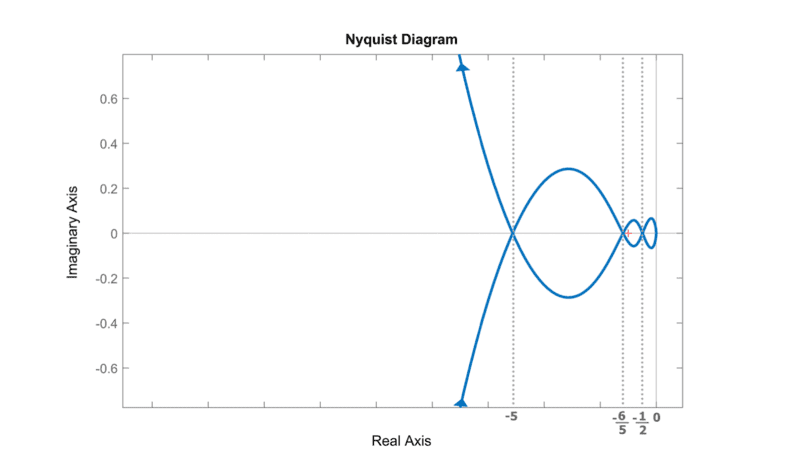
Point −1 is marked with a (small) cross and can also be obtained via the scale on the Re-axis.
i) Use the Nyquist curve in Figure 3 to determine how many zeros the system has.
------------------------------------------------------------------------------------------------
My attempt:
Why the point -1 was given is for a later task when you are supposed to check stability which I might need help with later. Anyway, this is a problem on an old exam so I already know the answer is 2 but I don't know how they know that from the given nyquist diagram. I know what a nyquist diagram and bode plots are but I don't know how they got to that answer. We can see from the diagram that there is at least one zero since G(iw) goes through the origin. That zero is probably when w=0 because the diagram looks completely symmetrical around the real axis. But maybe the other zero is of the form a+wi, a is not 0. I would not be able to find a zeros that has a real part from the nyquist diagram. Of course we don't need to find the other zero they only ask us how many zeros there are but I don't know how to determine that there are 2 zeros.
Thanks in advance!
Point −1 is marked with a (small) cross and can also be obtained via the scale on the Re-axis.
i) Use the Nyquist curve in Figure 3 to determine how many zeros the system has.
------------------------------------------------------------------------------------------------
My attempt:
Why the point -1 was given is for a later task when you are supposed to check stability which I might need help with later. Anyway, this is a problem on an old exam so I already know the answer is 2 but I don't know how they know that from the given nyquist diagram. I know what a nyquist diagram and bode plots are but I don't know how they got to that answer. We can see from the diagram that there is at least one zero since G(iw) goes through the origin. That zero is probably when w=0 because the diagram looks completely symmetrical around the real axis. But maybe the other zero is of the form a+wi, a is not 0. I would not be able to find a zeros that has a real part from the nyquist diagram. Of course we don't need to find the other zero they only ask us how many zeros there are but I don't know how to determine that there are 2 zeros.
Thanks in advance!