MattDutra123
- 15
- 0
- Homework Statement
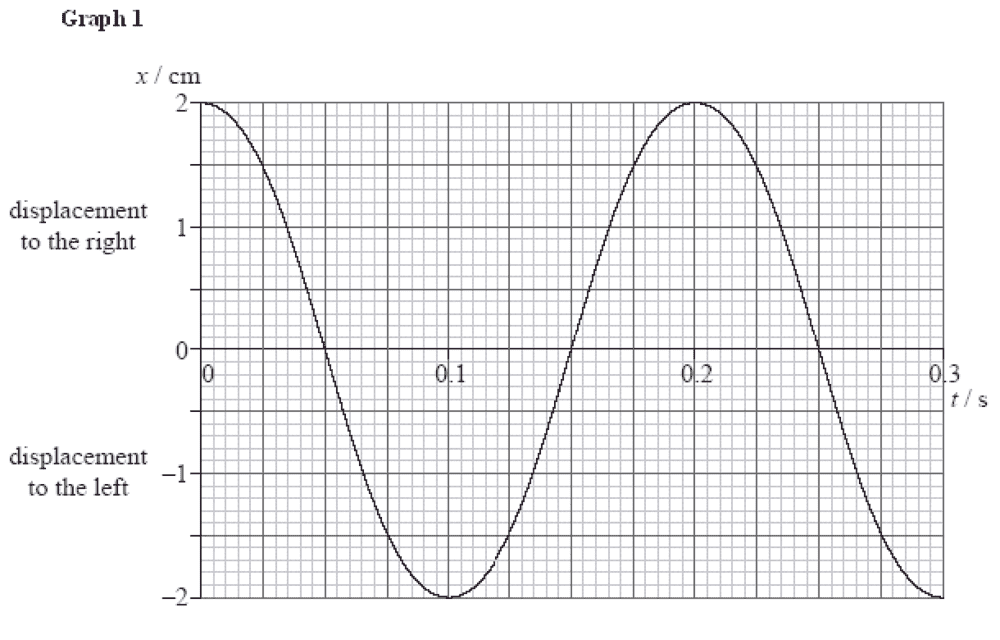
- Find the speed of this longitudinal wave at t=0.12s.
- Relevant Equations
- v=w*xmax*cos(wt)
The graph provided is below. The problem asks for the speed of the wave at 0.12s. I used the formula v=w*xmax*cos(wt), provided in our textbook where xmax is the amplitude of 2 cm, w (omega) is 2pi divided by the period of 0.2. However, for some reason this formula doesn't give me the correct result. Instead, the solution to the problem involves the formula w*sqrt(xmax^2-x^2), which requires us to first find the displacement at t = 0.12.
My question is: why does the formula I used not work? Why must we use the other formula to solve this problem? I apologise for the bad formatting of the formulas.
My question is: why does the formula I used not work? Why must we use the other formula to solve this problem? I apologise for the bad formatting of the formulas.