Andrei0408
- 50
- 8
- Homework Statement
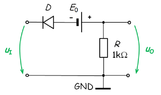
- The diode in the figure is described by its offset model: U_D0=0.6V and r_d=0. Knowing that E_0=3.9V, find the voltage threshold u_l, at which the diode switches to its opposite state.
- Relevant Equations
- u_l=−u_D−i_D * R
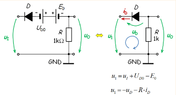
I've attached pictures with the circuit and part of the attempted solution. I've replaced the diode with its offset model and obtained the equivalent circuit in the 2nd picture. After applying KVL, I've obtained that u_l=−u_D−i_D*R. Since U_D0 is greater than 0, I've deduced that the diode must be ON in this case, therefore u_D=0, so u_l=−i_D*R. The problem is I don't know how to find i_D so I can calculate u_l. The answer for this problem should be, according to the book, −4.5 . Any ideas? Thank you!