How to find the work on an object on an inclined plane pulled with a rope

[Kelvin Andersen]

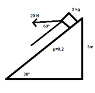
Homework Statement

g = $10m/s^2$
$\sqrt{3}$ = 1.7

Determine work by the 20N force

Homework Equations

for an inclined plane:

W = ((F+mgsin30)-(mgcos30)μ)s -> (Fx-ff)*s

for object pulled with angle:

W= (Fcos60-(mg-Fsin60)μ)s -> (Fx-ff)*s

The Attempt at a Solution

W= ((Fcos60+mgsin30)-(mgcos30-Fsin60)μ)s
(W= (Fx-ff)*s, Fx=Fcos50+wsin30, ff=(wcos30-Fsin60)*μ)

What I did to get the equation above:
for Fx:
Based on inclined plane equation, Fx=F+wsin30
However, since F is angled, F becomes Fcos60
so Fx=Fcos60+wsin30

for ff:
Based on angled force equation, ff=w-sin60
I change w -> wcos30
so ff=wcos30-Fsin60

sin30=3/s -> s=6
W= (((20)(cos60)+(3)(10)(sin30))-((3)(10)(cos30)-(20)(sin60))(0.2))(6) (inputting number based on the above)

by using √3 = 1.7

W= ((10+15)-(25.5-17)(0.2))(6)

W= (25-1.7)(6) = 139.8 Joules (don't know if correct or not)

 

[Abhishek kumar]

Homework Statement

View attachment 215645
g = $10m/s^2$
$\sqrt{3}$ = 1.7

Determine work

Homework Equations

for an inclined plane:

W = ((F+mgsin30)-(mgcos30)μ)s

for object pulled with angle:

W= (Fcos60-(mg-Fsin60)μ)s

The Attempt at a Solution

W= ((Fcos60+mgsin30)-(mgcos30-Fsin60)μ)s

W= (((20)(cos60)+(3)(10)(sin30))-((3)(10)(cos30)-(20)(sin60))(0.2))(3)

by using √3 = 1.7

W= ((10+15)-(25.5-17)(0.2))(3)

W= (25-1.7)(3) = 69.9 Joules (dont' know if correct or not)

Work done by which force you haven't mentioned

 

[PeroK]

Homework Statement

View attachment 215645
g = $10m/s^2$
$\sqrt{3}$ = 1.7

Determine work by the 20N force

Homework Equations

for an inclined plane:

W = ((F+mgsin30)-(mgcos30)μ)s

for object pulled with angle:

W= (Fcos60-(mg-Fsin60)μ)s

The Attempt at a Solution

W= ((Fcos60+mgsin30)-(mgcos30-Fsin60)μ)s

W= (((20)(cos60)+(3)(10)(sin30))-((3)(10)(cos30)-(20)(sin60))(0.2))(3)

by using √3 = 1.7

W= ((10+15)-(25.5-17)(0.2))(3)

W= (25-1.7)(3) = 69.9 Joules (don't know if correct or not)

The big problem with what you have posted is that you haven't explained at all what calculations you are carrying out. The line I've underlined is almost impossible to parse.

In any case, your solution looks wrong to me.

Try to explain what you are calculating and why.

 

[Kelvin Andersen]

The big problem with what you have posted is that you haven't explained at all what calculations you are carrying out. The line I've underlined is almost impossible to parse.

In any case, your solution looks wrong to me.

Try to explain what you are calculating and why.

edited

 

[PeroK]

edited

It's still incomprehensible to me.

How, in general, do you calculate the work done by a force?