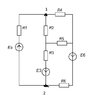
How to Find Voltage Between Node 1 and Node 2?

[builder_user]

Homework Statement

Find voltage between node 1 and node 2

Homework Equations

What is the algorithm?

The Attempt at a Solution

R1=4 Ohms
R2=5 Ohms
R3=8 Ohms
R4=3 Ohms
R5=6 Ohms
R6=7 Ohms
Eэ=20 V
E3=17 V
E5=15 V

 

[cupid.callin]

use balanced wheat stone bridge thing

 

[builder_user]

Do I need second Kirhgoff rules' equations for every loop?

 

[cupid.callin]

try "balanced wheat stone bridge"

you won't need Kirhgoff rules

here:http://en.wikipedia.org/wiki/Wheatstone_bridge

 

[tiny-tim]

hi builder_user!

Do I need second Kirhgoff rules' equations for every loop?

(Kirchhoff!)

'fraid so!

 

[builder_user]

What's the next step after Kirchgoff's rules?What do I need to find?I know current in every branch.

 

[gneill]

You want the voltage between nodes 1 and 2. Use the current you found for the first loop (leftmost) using Kirchhoff to determine the voltage across R1. Then do the obvious voltage sum.

 

[builder_user]

i1=3.7A

U=Eэ-i1*R1=5.2V?

And the final result -- 20(Eэ)+5.2(U)=25.2V?

 

[gneill]

That's not the value I get for i1. Better check your derivation.

EDIT: My error. Redoing my sums I see that i1 is indeed about 3.7A.

 

[builder_user]

That's not the value I get for i1. Better check your derivation.

Ok.But what's the next?

 

[gneill]

Ok.But what's the next?

The next what? Wasn't it the voltage between nodes 1 and 2 that you were looking for?

 

[builder_user]

but i's only I1.
Or R1*I1 - is the result?

 

[gneill]

Very sorry. I see that your figure of 3.7A for i1 and about 5.2V for the voltage between nodes 1 and 2 look okay.

 

[builder_user]

Very sorry. I see that your figure of 3.7A for i1 and about 5.2V for the voltage between nodes 1 and 2 look okay.

A-a-a-a-a!OMG!I'm already started to do all my work from the beginig...It's about 15 pages A4!

 

[gneill]

Again, sorry about that.

15 pages of A4? That seems like a lot for just three loops. What method are you using to solve the equations?

 

[builder_user]

Again, sorry about that.

15 pages of A4? That seems like a lot for just three loops. What method are you using to solve the equations?

It's a big work like coursework.I have 8 exercises need to do with this scheme(different trasformations like triangle-star and different methods of finding currents like method of equivalent generator(I don't know how does it called in English.translate from russian),node voltage method and etc.).And another 7 schemes.One of them is my previous topic's scheme.

I got this result(3.7) by different methods.So if it's wrong - all my work is wrong

 

[gneill]

I see, so this is just one exercise for the given schematic.

It seems to me that a KVL loop approach is the most straight forward for this particular question, since you really only need to solve for the current in the first loop. Have you learned the method to directly write (by inspection) the matrix form of the equations? That allows you solve for the currents using a matrix method (such as Cramer's Rule), which takes only a few lines.

 

[builder_user]

if it's cramer's method...
I know this method but I only use it in programming.I solve all equtations in MathCAd.And then I show result without numbers and then the final result.The result without numbers is very big sometimes.

 

[gneill]

Okay, even better.

Attached is an example, using MathCad, of solving the loops by writing the loop equations in matrix form (which can be done by inspection, and is (almost) foolproof). It's very quick.

 

[builder_user]

Intersting.I didn't know about it in Mathcad
all results are the same as the results in my method of countour currents

thank you for your help.

 

[gneill]

The most interesting part, I think, is that you can write the equation quickly by inspection.

For the impedance matrix, the terms on the diagonal are just the sum of the impedances (resistances in this case) in the given loop. The off-diagonal terms are just the negative of the impedances that are shared by the loops indexed by the matrix entry. So in this case, for example, R2 is shared by loops 1 and 2, so z₁₂ and z₂₁ are both -R2. Note that the impedance matrix is symmetrical about the diagonal, so it's very quick to fill in.

The voltage vector is just the sum of the voltage source rises in the given loop (where a rise is taken to mean that a given voltage source goes from - to + in the direction of the loop current).

 

[builder_user]

The most interesting part, I think, is that you can write the equation quickly by inspection.

For the impedance matrix, the terms on the diagonal are just the sum of the impedances (resistances in this case) in the given loop. The off-diagonal terms are just the negative of the impedances that are shared by the loops indexed by the matrix entry. So in this case, for example, R2 is shared by loops 1 and 2, so z₁₂ and z₂₁ are both -R2. Note that the impedance matrix is symmetrical about the diagonal, so it's very quick to fill in.

The voltage vector is just the sum of the voltage source rises in the given loop (where a rise is taken to mean that a given voltage source goes from - to + in the direction of the loop current).

I've got it.I compared elements of matrix with my equations a few minutes ago.