Elvis 123456789
- 158
- 6
Homework Statement
Finding "polar" and "rectangular" representation of a complex number?
Make a table with three columns. Each row will contain three representations of a
complex number z: the “rectangular” expression z = a + bi (with a and b real); the “polar”
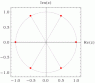
expression |z|, Arg(z); and a little picture of the complex plane with the complex number
marked on it. There are five rows, containing, in one column or another, the following
complex numbers:
(iv) A sixth root of 1 with argument θ such that 0 < θ < π/2
Homework Equations
I don't know if de moivre's theorem for Nth roots of complex numbers is relevant here
The Attempt at a Solution
I know that the modulus of Z = r = 1^(1/6) = 1 but I don't know how to find the Argument of Z
Z = 1^(1/6) e^(iθ)
Last edited by a moderator: