How to Solve Beam Problems with Step-by-Step Guidance and Free Diagrams?

  • Thread starter Thread starter Rambo12
  • Start date Start date
  • Tags Tags
    Beam
AI Thread Summary
To solve beam problems effectively, step-by-step guidance is essential, especially for those without access to personal instruction. Free diagrams significantly enhance understanding of concepts like shear force and bending moments. Resources such as Civil-Guy's introduction and links to educational websites provide valuable information and examples. These materials can aid in grasping the structural basics necessary for tackling beam problems. Utilizing these resources will facilitate a clearer understanding of the subject matter.
Rambo12
Messages
1
Reaction score
0
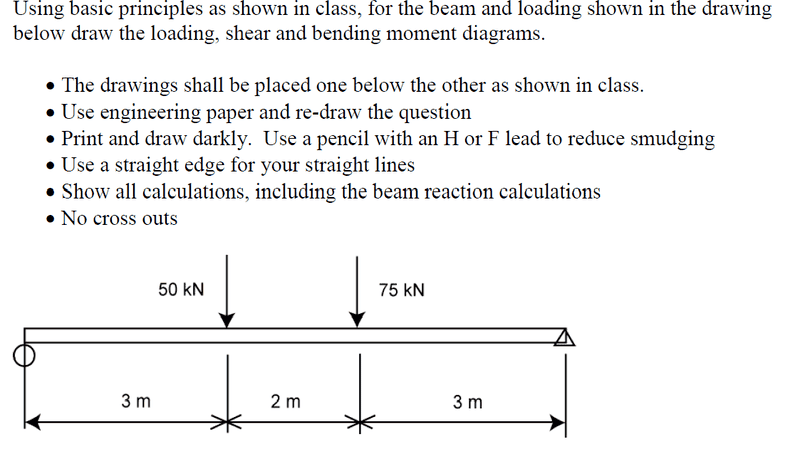
I am having problems solving this questions and I would appreciate it if someone teaches me step by step as I have no one to teach me at home.

Free diagrams would be really helpful too.

thanks everyone.


6pw4N.png

 
Physics news on Phys.org

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Distributed weight of inclined beam.
Replies
11
Views
3K
Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
1K
How to approach dynamics problems?
Replies
8
Views
2K
Solve 2D Asteroid Problem: Step-by-Step Guide
Replies
3
Views
2K
Calculating the sum of displacement vectors
Replies
5
Views
758
Having a hard time learning Newton's 2nd law
Replies
5
Views
2K
How can I solve this physics problem step by step?
Replies
2
Views
870
Free Body Diagram of Mass-Spring System
Replies
5
Views
1K
Potential Mistake in Free-Body Diagram
Replies
5
Views
2K
Ruler measurements and knowing how many decimal places to include
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top