ryan578
- 3
- 0
Member advised to use the homework template for posts in the homework sections of PF.
Hi I am new the site and have to complete this physics summer work from a not so clear textbook. I am also new to a lot of the concepts and material. I was unsure on how i go about solving velocity a and b in this problem:
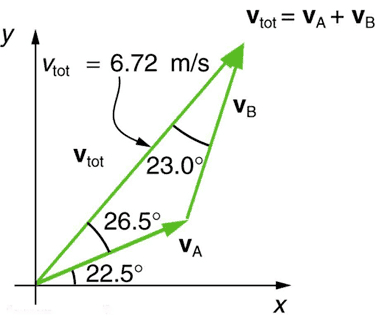 any help is appreciated
any help is appreciated
