cheddar87
- 7
- 0
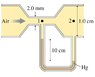
1. Air at 0∘C flows through the tube shown in the figure. Assume that air is an ideal fluid. What is the air speed v1 at point 1?2. Formulas: A1V1=A2V2, ΔP + 1/2ρΔV2, ρgΔh3. My first through process was to calculate the change in pressure in the mercury as the change in pressure in the mercury would correspond to the change in pressure from points 1 to 2. So i did this using ΔP+ ρgh=0 and calculated the Δp= 13,328 Pascals or .1315 atms. Then this is where i got stuck. I am not sure what to do now that I have the change in pressure. I thought my next step would be:
ΔP+ 1/2ρΔV2------> ΔP= -1/2ρΔV2----> 13,328=-1/2ρΔV2
to calculate the change in velocity from points 1 to 2 but I got caught up in units and the calculations ended up being messy so I don't think I am on the right track. I know I have the areas and I am sure those will come into the equation when I find one of the velocities but I am kind of stuck at this point
ΔP+ 1/2ρΔV2------> ΔP= -1/2ρΔV2----> 13,328=-1/2ρΔV2
to calculate the change in velocity from points 1 to 2 but I got caught up in units and the calculations ended up being messy so I don't think I am on the right track. I know I have the areas and I am sure those will come into the equation when I find one of the velocities but I am kind of stuck at this point