Ideal gas behaviour at high pressures

[Amith2006]

Sir,
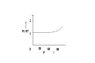
An experiment is carried on a fixed amount of gas at different temperatures and at high pressure such that it deviates from the ideal gas behaviour. The variation of PV/RT with P is shown in the following diagram. Is it right? Suppose a graph is plotted between PV/RT and T. At high temperatures, will the graph be identical to that between PV/RT and P i.e. will the value of PV/RT increase?

 

[maverick280857]

I haven't seen your graph yet but if you follow the van der Wall model, then Z = PV/RT is the compressibility factor. Z can vary with P in many ways depending on the gas (whether attractive forces dominate or whether the pressure is very high). This can be mathematically justified.

 

[Amith2006]

Sir,
Actually in the question 4 curves were given from which it was asked to choose the curve which more closely suits the situation described in the question. I have shown only the curve that was said to be right according to my book. From the graph, it seems that the compressibility is constant at low pressures but increases at high pressures. So can I take that the compressibility factor(PV/RT) remains constant at low pressures but increases at high pressures in the case of ideal gases?

 

[maverick280857]

Sir,
Actually in the question 4 curves were given from which it was asked to choose the curve which more closely suits the situation described in the question. I have shown only the curve that was said to be right according to my book. From the graph, it seems that the compressibility is constant at low pressures but increases at high pressures. So can I take that the compressibility factor(PV/RT) remains constant at low pressures but increases at high pressures in the case of ideal gases?

For an ideal gas, Z is independent of pressure. This is obvious becuse for one mole of gas, PV=RT so Z=1. So for an ideal gas, the Z versus P graph is a straight line for all pressures with Z = 1. Every non-ideal gas deviates from this straight line. So your gas is non-ideal, its just that non-ideality is exhibited above 60 pressure units (or maybe something just above it).

If you are using a vanderwall model, then you can expand Z as a power series (known as a virial equation) and play around with the coefficients so that the graph is almost linear until the point where it takes a hike

Read the following only if you're familiar with vanderwall's model.

Vanderwall's equation (1 mole of gas):

(P + \frac{a}{V^2})(V-b) = RT

if you neglect b (see your textbook for a justification),

P = \frac{RT}{V}-\frac{a}{V^2}
so,
Z=\frac{PV}{RT}=1-\frac{a}{VRT}

This actually shows that you can't neglect b for your gas because according to this assumption Z < 1, contrary to the observation. So I really should've written this as

P =\frac{RT}{V-b}-\frac{a}{V^2}

I'll leave the rest to you.