Impulse applied to an elastic pendulum

[montrex]

Homework Statement

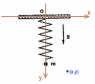
A pointlike body of mass $m=100$ $g$ is attached to the extremity of an ideal spring, whose constant is $K$ and its length at relaxed position is negligible. The other extremity of the spring is attached to the fixed point $O$.
At first the body mass, on which the gravitational force and elastic force act, is at rest on the vertical plane.
An horizontal impulse $\vec J= 1$ $Kg \frac{m}{s}$ acts on the body in a negligible time.
$(a)$ Evaluate the maximum distance of the body from $O$, specifying the trajectory of his motion.
$(b)$ If the impulse acts at $30°$ grades respect to the horizontal direction, as in the picture, evaluate the minimum depth reached by $m$ respect to the altitude of $O$.

Homework Equations

Hooke's law $\vec F = - K \vec x$
Conservation of energy $\Delta K +\Delta U_{g} +\Delta U_{e} =0$; where $K$ is the kinetic energy of the body, $U_{g}$ is its gravitational energy and $U_{e}$ is the elastic energy of the spring
Impulse $\vec J$ produced from time $t_{1}$ to $t_{2}$: $\vec J=\int \vec F \, dt = \Delta \vec p$

The Attempt at a Solution

This is what I thought. At the beginning, the body is at rest and the only forces are the gravitational and the elastic ones, which operate on a vertical axis. Thus, $mg-kL_{0}=0$, where $L_{0}$ is the elongation of the spring at first. It is important to remember that its length at relaxed position is negligible, as hypothesis.
$(a)-(b)$ Due to the impulse, the body has initial velocity $V_{0}= \frac {I}{m}$, with the same direction of $\vec J$. When it reaches the longest distance from $O$, its velocity $V_{f}=0$. Since there is a spring and not a simple rope, I am not able to relate the height reached by the body to the streching of the spring.
Thanks for considering my question, any suggestion for the problem or better translation is welcolmed.

 

[TSny]

Hello, montrex. Welcome to PF!

I would suggest that you figure out the shapes of the trajectories of the mass for parts (a) and (b) by finding the Cartesian coordinates x(t) and y(t) of the mass as functions of time.

You might introduce Cartesian axes as shown below.

If the mass is located at general coordinates (x,y), what are the x and y components of the net force acting on the mass? Express in terms of x and y and parameters of the system.

 

[montrex]

Hi, thanks. I have calculated the net force on both axes and it results:
$F_{x}=-Kx$ $\vec i$ and $F_{y}=mg-Ky$ $\vec j$. Since in $(a)$ the impulse is horizontal, the mass will remain on the same coordinate $y=L_{0}$ because $F_{y}=mg-Ky=mg-KL_{0}=0$. Thus, during the motion $\Delta U_{g}=0$ and it is possible to evaluate the maximum elongation by $\Delta K +\Delta U_{e} =0$.
In case $(b)$ the impulse is not parallel to an axis and the acceleration as expressed before depends by its position $(x,y)$. I have some difficulties in finding the coordinates of the mass as functions of time. I did not calculate them in point $(a)$ because I thought that the mass stays at the same $y$, but I am not sure about that.

 

[TSny]

Hi, thanks. I have calculated the net force on both axes and it results:
$F_{x}=-Kx$ $\vec i$ and $F_{y}=mg-Ky$ $\vec j$. Since in $(a)$ the impulse is horizontal, the mass will remain on the same coordinate $y=L_{0}$ because $F_{y}=mg-Ky=mg-KL_{0}=0$. Thus, during the motion $\Delta U_{g}=0$ and it is possible to evaluate the maximum elongation by $\Delta K +\Delta U_{e} =0$.

Yes, good.

In case $(b)$ the impulse is not parallel to an axis and the acceleration as expressed before depends by its position $(x,y)$. I have some difficulties in finding the coordinates of the mass as functions of time. I did not calculate them in point $(a)$ because I thought that the mass stays at the same $y$, but I am not sure about that.

For this part, you might try using a coordinate system with origin at the equilibrium position of the mass. Let coordinates of a point in this system be (X, Y) . What do you discover if you express the X and Y components of the net force in terms of the coordinates X and Y instead of x and y?
[You won't actually need to find X and Y as explicit functions of time in order to answer the problem statement. But you can if you wish.]