Inclined Plane Newton's Law Problem

[vladimir69]

Homework Statement

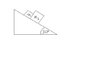
Check out my attachment to get an idea what is happening. What we have is an inclined plane with 2 masses (m1 and m2) which are touching one another and the angle of the incline is 30 degrees.
The coefficient of kinetic friction between m1 and the plane is 0.23 = mu_k1
The coefficient of kinetic friction between m2 and the plane is 0.51 = mu_k2
m1 = 2.5kg
m2 = 3.1kg
theta = 30 degrees
The question is to find the acceleration of the pair of masses, and the second question is find the force of m1 on m2

Homework Equations

F=ma

The Attempt at a Solution

I applied Mr Newton on each mass individually to get
for mass m1:
x direction (parallel to the inclined plane):
-F_{21}-\mu_{k1}N_{1}+m_{1}g\sin(30)=m_{1}a
y direction (perpendicular to the inclined plane):
-m_{1}g\cos(30)+N_{1}=0

for mass m2:
x direction:
F_{12}-\mu_{k2}N_{2}+m_{2}g\sin(30)=m_{2}a
y direction:
-m_{2}g\cos(30)+N_{2}=0

I used F_{12}=-F_{21}.

I put all that into the mix and out popped a = 9.33m/s^2, which is wrong.
The answer says a = 1.6m/s^2. I am pretty sure my maths is ok. I'd say the problem is in my application of Newton but can't see anything wrong.

Thanks in advance

 

[Chi Meson]

Well, I don't know what you did to get that answer.

On all these "sliding down incline" problems, you usually can assume that all forces perpendicular to the surface will balance, so all you need to look at the parallel forces.

I can't tell if you allowed the normal forces between blocks to cancel each other. You should have.
Did you substitute m_g{1}\cos(30) for the N to find the frictional force? (for each block?

Did you divide the net force by the total mass?

I can't tell what you did.

 

[alphysicist]

Hi vladmir69,

I noticed that you said that F_{12}=-F_{21}; I think that is where your error is, because with the notation you have in your problem that is not quite true.

What is true is that \vec F_{12}= - \vec F_{21}; the vectors are equal in magnitude and opposite in direction. But in your equations, F_{12} and F_{21} just represent the magnitudes of those forces; you have already taken care of the direction by making one term negative and one term positive. Now you just have to force the magnitudes to be equal, so you need to use F_{12}= F_{21}.

 

[vladimir69]

thanks alphysicist you have solved the problem