- #1
zorro
- 1,384
- 0
Homework Statement
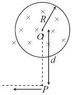
In a cylindrical region of radius R, there exists a time varying magnetic field B such that dB/dt=k(>0) . A charged particle having charge q is placed at the point P at a distance d (> R) from its centre O. Now, the particle is moved in the direction perpendicular to OP (see figure) by an external agent upto infinity so that there is no gain in kinetic energy of the charged particle. Show that the work done by the external agent is independent of d and find it.
The Attempt at a Solution
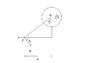
Let the angle between the line joining the particle to the point O make an angle θ with the vertical.
∫E.dl=-kπR2
E*x*cos(180-θ)=-kπR2, where x is horizontal distance of the particle from the initial position.
Substituting x for dtanθ and solving, I get W= qkπR2 which is incorrect.
The answer given is qkπR2/4