See:
https://www.physicsforums.com/threa...duction-lecture-16.948122/page-6#post-6857043
You might find this thread of interest=look at in particular posts 187, 188, 189, and 194. There doesn't seem to be complete agreement in the Physics Forums regarding this topic, but you still may find this of interest. It is up to the individual to ultimately determine what is good physics and what isn't.
Note: I got the necessary edits in to these posts before the thread was closed. I stick by my conclusions on this. We don't have complete agreement with everyone, but that is ok.
I did a repeat of post 27 of this thread here, because the discussion in the thread that is linked is closely related to what we discussed in the last several posts. I think for the most part, we have discussed Professor Lewin's paradox more than enough, but for completeness I thought I would include this one more time. I'm not sure if anyone might want to comment further, but for a couple of the items, posts 187, 188, 189, and 194 in the linked thread, I would welcome any feedback. The case of the coil with several or many turns is slightly different than Professor Lewin's single open ring, and it appears we do have some agreement now on what the results would be.
Edit: It should be noted that the thread that is linked above was closed, mostly due to some large disagreement that there was at the time. It looks to me though that some of the issues are finally getting resolved, and we are seeing more agreement.
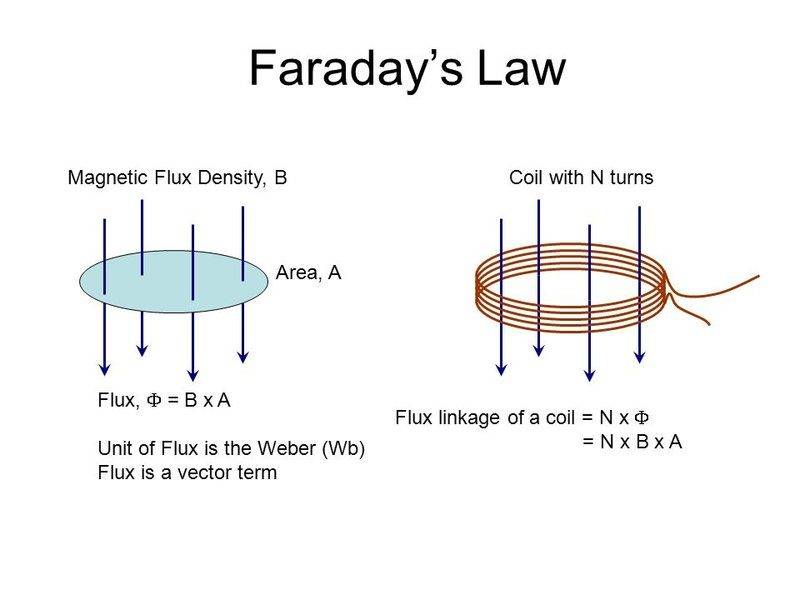
additional comment: Using ## \int E_s \, dl ##, we now IMO have a more complete explanation for what is going on with the inductor, than somewhat logically, but seemingly an incomplete explanation of multiplying the changing flux by the number of turns ## N ## to get the emf. It left open what to do in the case that there is e.g. ## N=2.5 ## turns. With the introduction of ## E_s ## and ## E_{induced} ## we can more accurately predict and calculate what will result in some of these cases.
@vanhees71 @alan123hk I added a few things, edits, etc., in both posts 41 and 42 that might be of interest that you may not have seen yet. I welcome any feedback you may have, but I am already pleased with the feedback you have provided so far. :)
Edit: One more item worth mentioning is that for the path consisting of the voltmeter resistor and the voltmeter wires, we have Ohm's law: ## \int E_{total} \, dl=IR=V_{measured} ##.