Inertia of a Giraffe in Terms of a Monkey (I'm serious)

[B3NR4Y]

Homework Statement

For my second thread of the day I will give the weirdest problem I've encountered in physics yet.
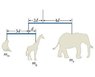
In the mobile what is the inertia of the giraffe m_gir in terms of the inertia m_m of the monkey?

Homework Equations

I = md²

The Attempt at a Solution

In the picture, the giraffe and monkey are on their own rod type thing, each 2-d away. So the inertia of both are m_m 4 d² = I_m and m_gir 4 d² = I_gir. It says to find the inertia of the giraffe in terms of the inertia of the monkey, but I don't really have any equations that relate the two as far as I know (other than the inertia of the whole system, but I don't know what that is equal to and that seems like it would lead me down a fruitless path). Can I even calculate inertias of objects individually? This isn't too clear to me.

 

[haruspex]

I think you are supposed to assume the mobile will hang balanced if still. This allows you to deduce the relationship between the three masses.
You don't state explicitly an axis for rotational inertia. There's no physical axis that they are both 2d from. Have you posted the whole question, word for word? Are you sure it's asking about rotational inertia?