Infinite sheet of chargejust on sigma stuff

[rdn98]

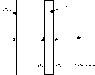
An infinite nonconducting sheet of charge, oriented perpendicular to the x-axis, passes through x = 0. It has area density s1 = -3 µC/m2. A thick, infinite conducting slab, also oriented perpendicular to the x-axis, occupies the region between x = a and x = b, where a = 3 cm and b = 4 cm. The conducting slab has a net charge per unit area of s2 = 4 µC/m2.

a picture is added below
===============
(b) Calculate the surface charge densities on the left-hand (sa) and right-hand (sb) faces of the conducting slab.You may also find it useful to note the relationship between sa and sb.

sa=?
sb=?

where s stands for sigma
==========
Ok, so I need to figure out the two indivudal surface charges, that will give me the net overall surface charge density.
I know that E=sigma/ (2*epislon)
where E = electric field
epislon= 8.85e-12

I can figure out the electric field values between the two slabs, and the electric fields to the right of the conducting slab.

Total Electric field for slab 1 = sigma_1/(2*epsilon) = -1.69E5 N/C =E_left
Total Electric field from slab 2 is sigam_2/(2*epsilon) = 2.25E5 N/C = E_right

now, I tried setting up this equation
for the left side of slab 2
-E_right+E_left=(sigma_1+sigma_2)/(2*epsilon)

now to the right side of slab 2
E_right+E_left=(sigma_1+sigma_2)/(2*epsilon)

so its a system of equations..but when I solve for one sigma, it totally cancels itself out when plugged into the other equation..I've been at this stupid problem for almost an hour and half..how do I finish this ?

 

[turin]

Don't imagine σ₂ as inside the dotty region. The conducting slab is a conductor, so what does that tell you about the charge inside? What does it tell you about the electric field inside? Use superposition to satisfy the condition for the electric field inside the conductor.

I only see one one σ for the conducting slab, but there should be two; one for the left side and one for the right side. The σ for the x = 0 plane is a given constant.

One more thing, you have that the conducting slab is an infinite slab, but the picture depicts a finite slab. This may cause confusion.

 

[rdn98]

I love it how people ask me these questions, and yet, I do not even know if I have the right answer. Ok, I have the net sigma charge for the 2nd slab, and I need to break it up into two individual parts, sigma_a and sigma_b, where 'a' is left side of slab2, and 'b' is right side of slab 2.


I know that the electric field inside a conduction is 0...so how is that going to help me find sigma_a and sigma_b?

 

[Doc Al]

so its a system of equations..but when I solve for one sigma, it totally cancels itself out when plugged into the other equation..I've been at this stupid problem for almost an hour and half..how do I finish this ?

Write two equations to represent these facts:
(1) The field inside the conductor must be zero. (The net field is due to the three surface charges.)
(2) The total surface charge on the conductor is 4 µC/m2.