Initial energy stored in springy steel before oscillating

[Janiceleong26]

1. Homework Statement

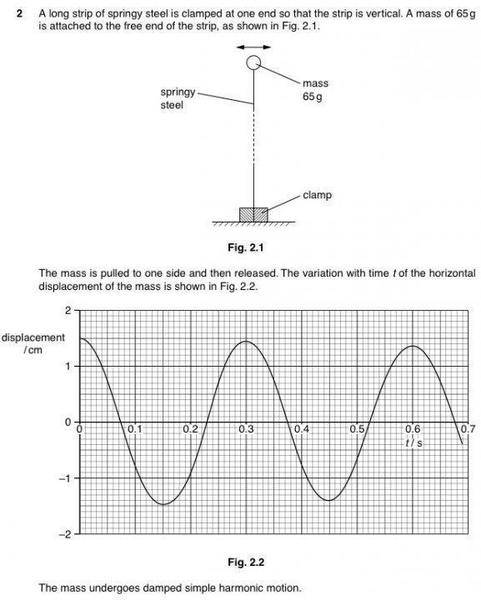
Ok so, for part b ii)
The solution did this :
1/2 (0.065) (2π /0.3)² (1.5 x 10^-2)², which is the KE of the mass when its speed is max.
But why do they calculate the energy when it is at its equilibrium position where its speed is max?
I assume that the energy before release is equal to the energy when it passes through the equilibrium position as there is no energy lost.. But that can't be true because the mass undergoes damped simple harmonic motion.
Can someone please explain to me? Thanks in advance

 

[drvrm]

I assume that the energy before release is equal to the energy when it passes through the equilibrium position as there is no energy lost.. But that can't be true because the mass undergoes damped simple harmonic motion.
Can someone please explain to me? Thanks in advance

i do not think the assumption of energy before release converting to kinetic energy at equilibrium position is correct- the steel which is springy and its length will vary as it moves-v and some energy will be stored in the springy part- pl try to analyse the motion taking this fact into consideration- which leads to damping.

 

[haruspex]

But why do they calculate the energy when it is at its equilibrium position where its speed is max?
I assume that the energy before release is equal to the energy when it passes through the equilibrium position as there is no energy lost.. But that can't be true

It depends what you mean by the energy stored in a system. Batteries do not return all the energy put into them, so is the stored energy what you put in or what you can get out?

 

[Janiceleong26]

It depends what you mean by the energy stored in a system. Batteries do not return all the energy put into them, so is the stored energy what you put in or what you can get out?

Hmm..I guess it's what I can get out?

 

[Janiceleong26]

i do not think the assumption of energy before release converting to kinetic energy at equilibrium position is correct- the steel which is springy and its length will vary as it moves-v and some energy will be stored in the springy part- pl try to analyse the motion taking this fact into consideration- which leads to damping.

Could the assumption be true for the first half of the oscillation (t=0 to t=1.5)? Since the amplitude of oscillation is the same at the other half of the motion (see fig.2.2) ? So elastic PE stored before released = KE at equi. position?

 

[drvrm]

Could the assumption be true for the first half of the oscillation (t=0 to t=1.5)? Since the amplitude of oscillation is the same at the other half of the motion (see fig.2.2) ? So elastic PE stored before released = KE at equi. position?

i think it needs to analyze the situation from beginning-
1. when it was at rest initially at equilibrium draw the free body diagram and calculate the compression in spring.
2. as it is moved to 1.5 cm then again draw the free body diagram and calculate the compression in springy steel.
3. compare the energy at the two places - i think one can get the stored energy at the beginning of the motion.

 

[haruspex]

Hmm..I guess it's what I can get out?

With that definition, the energy at first peak velocity would be the right answer.
@drvrm, it is only possible to state the stored energy in one or other of those senses, either what was put in or what was got out. In between, an unknown amount of energy was turned into heat during the energy storage phase, and another unknown amount of energy was turned into heat in the extraction phase.
Perhaps you could assume that the same fraction of energy is lost in each phase. But it seems to me that the requirement in this thread is to explain the book answer.

 

[drvrm]

The solution did this :
1/2 (0.065) (2π /0.3)2 (1.5 x 10-2)2, which is the KE of the mass when its speed is max.

But it seems to me that the requirement in this thread is to explain the book answer.

check the above -does it come to 3.2 mJ?

 

[haruspex]

check the above -does it come to 3.2 mJ?

Yes. So?
Janice stated in the OP that the book answer was 3.2mJ, and that the way it was arrived at was by considering the stored energy to be equal to the KE at the first peak in KE. And as you note, that method leads to that answer. Her puzzlement is why the method is considered valid, given that there should be losses during the first quarter oscillation.
Instead of addressing that, you appear to have been arguing for calculating that loss.

 

[drvrm]

Yes. So?
Janice stated in the OP that the book answer was 3.2mJ, and that the way it was arrived at was by considering the stored energy to be equal to the KE at the first peak in KE. And as you note, that method leads to that answer. Her puzzlement is why the method is considered valid, given that there should be losses during the first quarter oscillation.
Instead of addressing that, you appear to have been arguing for calculating that loss.

No,Agrreing to your wise advice i just tried to get the number and i may be wrong i was getting 0.32 mJ that's why i called for the check.
if its all right -no problem.

 

[Janiceleong26]

With that definition, the energy at first peak velocity would be the right answer.

Oh I see.. Ok thanks a lot !

 

[haruspex]

No,Agrreing to your wise advice i just tried to get the number and i may be wrong i was getting 0.32 mJ that's why i called for the check.
if its all right -no problem.

Ah, ok. Do you get 3.2mJ now? I just checked it again, and I think it is right.

 

[Biker]

Ah, ok. Do you get 3.2mJ now? I just checked it again, and I think it is right.

No gravity in the problem?

 

[haruspex]

No gravity in the problem?

That gets tricky. If we assume the strip is uniform but massless, its displacement at a given point will be a cubic function of its distance from one end. Not sure how that turns into a restorative force at the mass.
If we pretend it's like an inverted pendulum, i.e. the strip remains straight and flexes from the base, all that does is reduce the effective spring constant, so still produces the damped harmonic oscillation. The gained PE in going from flexed to vertical would then have to be added to the peak KE to find the energy released by the spring.
With a more realistic behaviour of the strip, I think it comes down to finding the curve length of a cubic, which is nasty.