- #1
VVS
- 91
- 0
Hi,
I have already evaluated the integral 1/sqrt(x)exp(-ix) using The Residue Theorem and now I was looking for another method. So I thought of applying integration by parts and I got this attached formula.
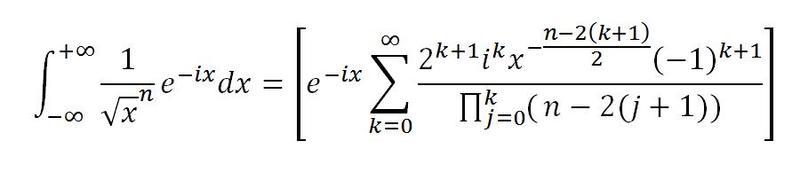
Now I am wondering how to evaluate this series. My first doubt is whether it converges or not.
Actually I just want to evaluate it for n=1.
Does anyone have any ideas? Can this sum be expressed as an integral?
Thank you
Homework Statement
I have already evaluated the integral 1/sqrt(x)exp(-ix) using The Residue Theorem and now I was looking for another method. So I thought of applying integration by parts and I got this attached formula.
Now I am wondering how to evaluate this series. My first doubt is whether it converges or not.
Actually I just want to evaluate it for n=1.
Does anyone have any ideas? Can this sum be expressed as an integral?
Thank you