Finding the Fourier cosine series for ##f(x)=x^2##

In summary, the Fourier cosine series for the function \( f(x) = x^2 \) involves calculating the coefficients of the series over a specified interval, typically \( [0, L] \). The coefficients are determined using the formula \( a_n = \frac{2}{L} \int_0^L f(x) \cos\left(\frac{n \pi x}{L}\right) dx \). For \( f(x) = x^2 \), the series converges to the function in the interval and represents it as a sum of cosine terms. The resulting series provides a way to approximate the quadratic function using orthogonal cosine functions.
  • #1
chwala
Gold Member
2,753
388
Homework Statement
See attached.
Relevant Equations
Fourier cosine series
I was just going through my old notes on this i.e

1699522218550.png
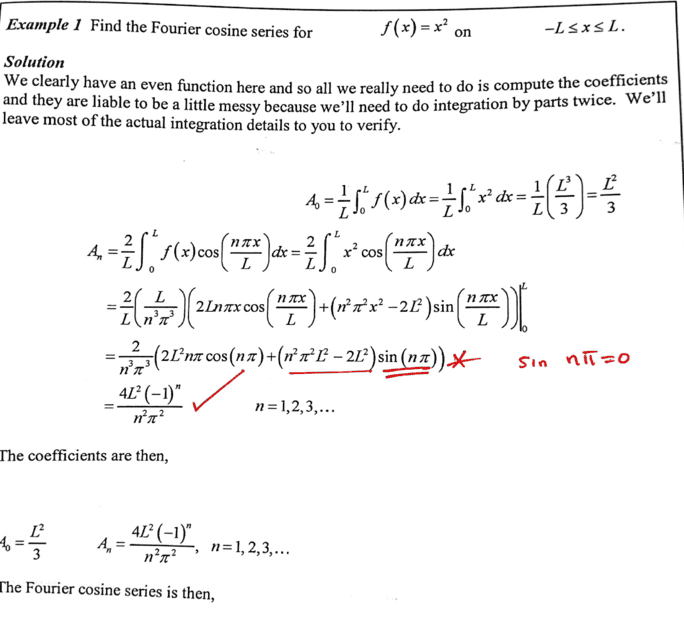The concept is straight forward- only challenge phew :cool: is the integration bit...took me round and round a little bit... that is for ##A_n## part.

My working pretty ok i.e we shall realize the text solution. Kindly find my own working below.

1699522329913.png
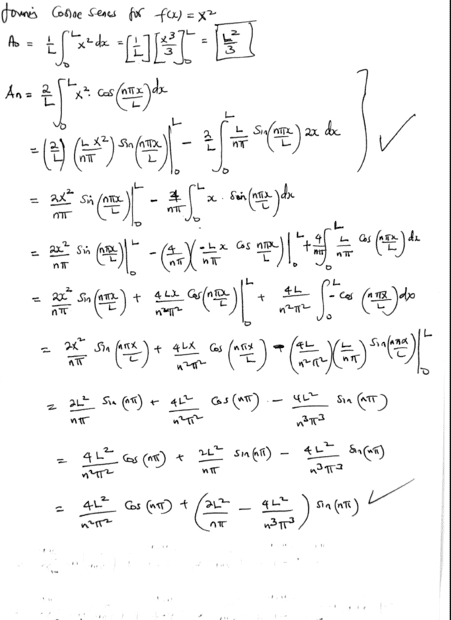Now to my question supposing we have to find say Fourier cosine series for ##f(x)= x^7##. The integration by parts here will take like forever to do. Do we have software for this? Will Wolfram help?
 
Last edited:
Physics news on Phys.org
  • #2
chwala said:
Will Wolfram help?
Pretty easy to check for yourself :wink: . Let us know !

##\ ##
 
  • #3
BvU said:
Pretty easy to check for yourself :wink: . Let us know !

##\ ##
Will do check @BvU ... however, if one was to do this by hand ... No technology...how long would it take to work to solution?
 
  • #4
The ##f(x)= x^7## is odd. Perhaps Fourier sine series rather than cosine?
 
  • Like
Likes chwala
  • #5
chwala said:
Now to my question supposing we have to find say Fourier cosine series for ##f(x)= x^7##. The integration by parts here will take like forever to do. Do we have software for this? Will Wolfram help?

Set [tex]I_n = \int_0^{2\pi} x^{2n+1} \sin kx\,dx, \qquad k = 1, 2, \dots.[/tex] so that integrating by parts twice, [tex]
I_n = - \frac{(2n+1)(2n)}{k^2}I_{n-1} - \frac{(2\pi)^{2n+1}}{k}.[/tex] This recurrence relation can be solved subject to the initial condition [itex]I_0 = -\frac{2\pi}{k}[/itex] to obtain [tex]
I_N = \frac{(2N + 1)!(-1)^N}{k^{2N}} \frac{2\pi}{k}\sum_{n=0}^N \frac{(-1)^{n+1}(2\pi k)^{2n}}{(2n+1)!}.[/tex]
 
  • Informative
  • Like
Likes chwala and DrClaude

FAQ: Finding the Fourier cosine series for ##f(x)=x^2##

What is the formula for the Fourier cosine series?

The Fourier cosine series for a function \( f(x) \) defined on the interval \([0, L]\) is given by:\[ f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos\left(\frac{n \pi x}{L}\right) \]where the coefficients \( a_n \) are calculated using:\[ a_n = \frac{2}{L} \int_0^L f(x) \cos\left(\frac{n \pi x}{L}\right) \, dx \]for \( n \geq 0 \).

How do you find the coefficient \( a_0 \) for \( f(x) = x^2 \) on the interval \([0, \pi]\)?

The coefficient \( a_0 \) is found by:\[ a_0 = \frac{2}{\pi} \int_0^{\pi} x^2 \, dx \]Evaluating the integral:\[ a_0 = \frac{2}{\pi} \left[ \frac{x^3}{3} \right]_0^{\pi} = \frac{2}{\pi} \cdot \frac{\pi^3}{3} = \frac{2 \pi^2}{3} \]Thus, \( a_0 = \frac{2 \pi^2}{3} \).

How do you find the coefficients \( a_n \) for \( f(x) = x^2 \) on the interval \([0, \pi]\)?

The coefficients \( a_n \) for \( n \geq 1 \) are found by:\[ a_n = \frac{2}{\pi} \int_0^{\pi} x^2 \cos\left(\frac{n \pi x}{\pi}\right) \, dx = \frac{2}{\pi} \int_0^{\pi} x^2 \cos(nx) \, dx \]This integral can be evaluated using integration by parts twice. The result is:\[ a_n = \frac{4(-1)^n}{n^2} \]for \( n \geq 1 \).

What is the importance of the Fourier cosine series?

The Fourier cosine series is important because it allows us to represent a function as a sum of cosines, which can simplify the analysis and solution of differential equations, signal processing, and other applications in physics and engineering. It is particularly useful for functions defined on a finite interval and symmetric about the y-axis.

Can you provide

Similar threads

Solving the Fourier cosine series
Replies
1
Views
1K
Why only odd cosine terms in this Fourier series?
Replies
1
Views
774
A few questions to make sure I understand Fourier series
Replies
3
Views
1K
Solve integral by finding Fourier series of complex function
Replies
3
Views
970
Fourier series for trigonometric absolute value function
Replies
8
Views
2K
Complex Fourier Series into a Cosine Series
Replies
15
Views
3K
Fourier series and the shifting property of Fourier transform
Replies
6
Views
1K
Determine Convergence/Divergence of Sequence: f(x)=ln(x)^2/x
Replies
34
Views
3K
Extending function to determine Fourier series
Replies
8
Views
2K
Solve the given differential equation
Replies
10
Views
1K

Hot Threads

Recent Insights

Back
Top