JMoody
- 6
- 0
Hello, I'm hoping somebody can give me some insight on how to solve this problem. This was a solid mechanics exam question and I wasn't able to finish it because I'm rather weak in math.
1. Homework Statement
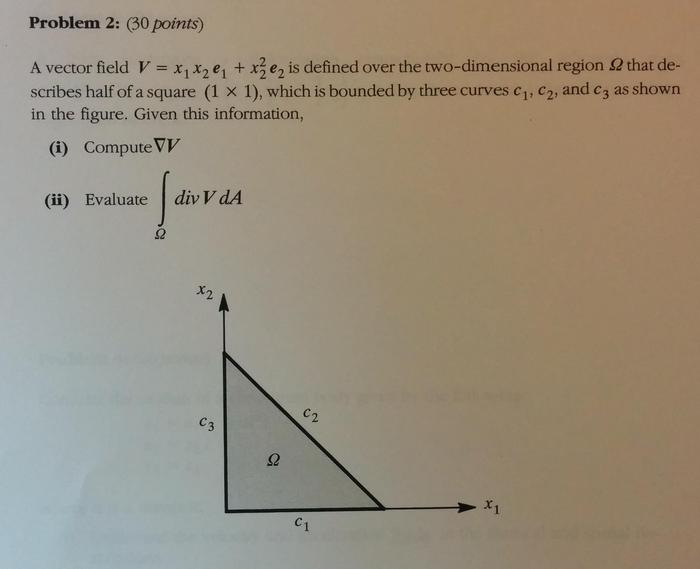
Recall divergence theorem for part ii. ∫div(V)dA = ∫V⋅ndS where n is normal to the surface.
Part i.
Not an issue, I can solve it easily.
Part ii.
I can apply divergence theorem no problem.
For the n vector field I get:
n1 = -e2
n3 = -e1
n2 = .707(e1 + e2)
The problem is that I've been out of school for quite a while, and I can't remember how to successfully integrate over the surface (perimeter) now. I realize I need to break it up into parts for each line of the surface, but it's been years since I've taken calculus.
1. Homework Statement
Homework Equations
Recall divergence theorem for part ii. ∫div(V)dA = ∫V⋅ndS where n is normal to the surface.
The Attempt at a Solution
Part i.
Not an issue, I can solve it easily.
Part ii.
I can apply divergence theorem no problem.
For the n vector field I get:
n1 = -e2
n3 = -e1
n2 = .707(e1 + e2)
The problem is that I've been out of school for quite a while, and I can't remember how to successfully integrate over the surface (perimeter) now. I realize I need to break it up into parts for each line of the surface, but it's been years since I've taken calculus.
Last edited: