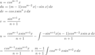Integrate: ## \int \cos^m(x)\sin^n(x)~dx ##

[Fatima Hasan]

Homework Statement

Derive that:

Correction (from a later post)
The integral on the left side should be $\int \cos^m(x)\sin^n(x)~dx$

Homework Equations

-

The Attempt at a Solution

Anyone can help me on how to start?

$u = cos^m x$

$du = m cos^{m-1} x$

$dv = sin^n x dx$

$v = \frac{sin^{n+1} x}{n}$

 

[BvU]

Hi,
$du = m \cos^{m-1} x$ can not be correct; the left hand side is a differential and the right hand side is not. Also, it is clearly wrong for $m = 1$ ...

 

[Fatima Hasan]

Hi,
$du = m \cos^{m-1} x$ can not be correct; the left hand side is a differential and the right hand side is not. Also, it is clearly wrong for $m = 1$ ...

How to derive $u = cos^{m} \,\,\, x$ ?

 

[BvU]

You use the chain rule

 

[Fatima Hasan]

You use the chain rule

 

[BvU]

Now that we have settled that: is there a typo in the problem statement ? On the left I see no variable $n$ !?

 

[Fatima Hasan]

Now that we have settled that: is there a typo in the problem statement ? On the left I see no variable $n$ !?

yeah , it should be ∫cos^mx sinⁿdx

 

[Fatima Hasan]

 

[BvU]

Doesn't look like the expression in post #1 yet, does it ?
What could be the trick to get e.g. $m+n$ in the denominator ?

 

[Fatima Hasan]

How can I ?

 

[Ray Vickson]

How can I ?

You cannot. Your are being asked to show something that is false. If you let $L$ be your (corrected) left-hand-side and $R$ the right-hand-side, then trying out some small integer values of $m$ and $n$ will show that the result is wrong. For example:
$$\begin{array}{cl}
m=2,n=2: & L = -\frac{1}{4} \cos(x)^3 \sin(x)+ \frac{1}{8} \cos(x) \sin(x)+ \frac{1}{8} x&\\
& R = \frac{1}{4} \cos(x) \sin(x)^3- \frac{1}{8} \cos(x) \sin(x)+\frac{1}{8} x \\
m=5,n=3: & L = - \frac{1}{8} \cos(x)^6 \sin(x)^2- \frac{1}{24} \cos(x)^6 \\
&R = \frac{1}{8} \cos(x)^4 \sin(x)^4-\frac{1}{10} \cos(x)^3 \sin(x)^2- \frac{1}{15} \cos(x)^3
\end{array}
$$

You can check these using a computer algebra system; I used Maple, but you can do it (at no cost) using Wolfram Alpha, for example.

 

[Mark44]

Checking some online tables of trig integrals, I found this one that is nearly the same as that in the OP:

$$\int \cos^m(x)\sin^n(x)dx = \frac{\cos^{m-1}(x)\sin^{n+1}(x)}{m + n} + \frac{m - 1}{m + n}\int \cos^{m-2}(x)\sin^n(x)dx$$
The main difference between this integral formula and the one in post #1 is the exponent on the cosine factor in the last integral.
In post 1, the exponent is m - n. In the formulat just above, the exponent is m - 2. As @Ray Vickson points out, the integral as posted isn't correct, so it's very likely that the m-n exponent is a typo.