NihalRi
- 134
- 12
1. Homework Statement
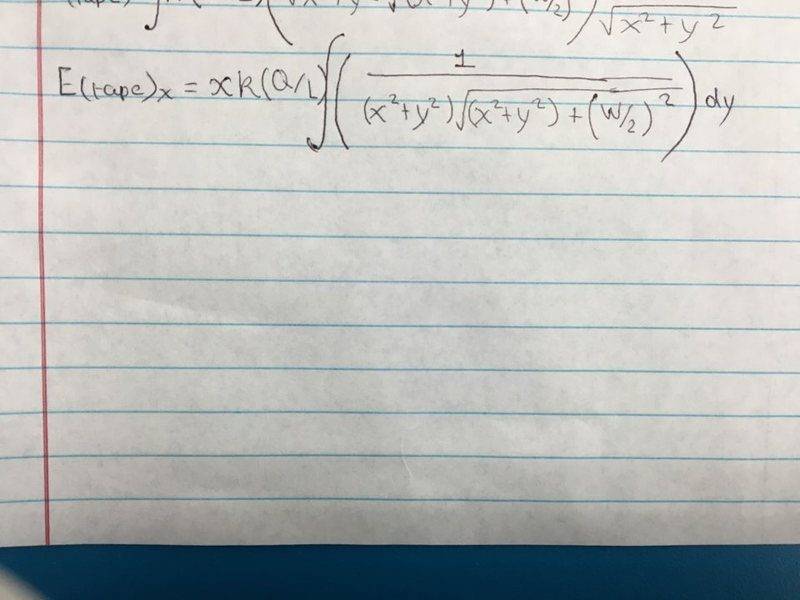
I'm trying to integrate this, the only variable is y the others(x,w) are all constants.
The ways of integrating that I am familiar with are substitution, trigonometric substitution, by parts & partial fraction decomposition.
Looking at this I can't think of where I'd begin, should I rearange? Is it multistep? It it possible ? I'd appreciate any help :)
I'm trying to integrate this, the only variable is y the others(x,w) are all constants.
Homework Equations
The ways of integrating that I am familiar with are substitution, trigonometric substitution, by parts & partial fraction decomposition.
The Attempt at a Solution
Looking at this I can't think of where I'd begin, should I rearange? Is it multistep? It it possible ? I'd appreciate any help :)