cromata
- 8
- 0
I am modeling some dynamical system and I came across integral that I don't know how to solve. I need to integrate vector function f=-xj+yi (i and j are unit vectors of Cartesian coordinate system).
I need to integrate this function over a part of spherical shell of radius R. This part is actually projection of circle (that lies in x-y plane) of radius 'b' on this sphere. I know that it's usually easier to integrate spherical shell in spherical coordinates but it's really tricky to set the intervals of integration in this problem in spherical coordinates.
-So my question is, is it possible to integrate this in Cartesian coordinates. Because i know integration intervals: I just need to set the interval for x and y as circle in x-y plane (z interval would be little tricky)
I also posted image so you can better see what the problem is...
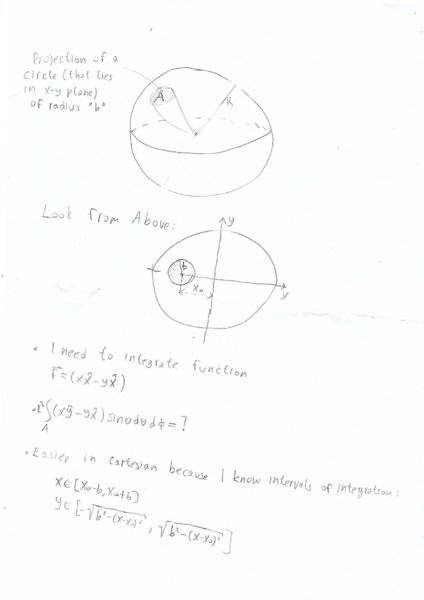
I need to integrate this function over a part of spherical shell of radius R. This part is actually projection of circle (that lies in x-y plane) of radius 'b' on this sphere. I know that it's usually easier to integrate spherical shell in spherical coordinates but it's really tricky to set the intervals of integration in this problem in spherical coordinates.
-So my question is, is it possible to integrate this in Cartesian coordinates. Because i know integration intervals: I just need to set the interval for x and y as circle in x-y plane (z interval would be little tricky)
I also posted image so you can better see what the problem is...
