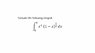Integration problem : Beta function related

[Alhussein]

Homework Statement

the problem is in the figure

Homework Equations

beta function = ∫u^x-1 * (1-u)^y-1 du " the integral is form 0 to 1"

The Attempt at a Solution

to use the beta function the integral must be from 0 to 1 but this problem is from 0 to a
so i let X^2=a^2 * t
and i got from it x, dx . the integral became from 0 to 1 and everything seemed fine till i found that the (1-x)^0.5 will be (1-a root t)^0.5 which isn't the general forum of the beta function. so i hope any1 will help me or tell me if there's another way to solve this integral without the beta function if it's possible

 

[Dick]

You could just do the u-substitution u=1-x. So just expand x^4=(1-u)^4 and integrate term by term.

 

[Alhussein]

You could just do the u-substitution u=1-x. So just expand x^4=(1-u)^4 and integrate term by term.

hmm ty for this answer it worked out well.but don't u know any solution for it by using beta function since the problem in the book was after that lesson

 

[Dick]

hmm ty for this answer it worked out well.but don't u know any solution for it by using beta function since the problem in the book was after that lesson

Well, your original integral is an 'incomplete beta function' if that's what your are after.

 

[Alhussein]

Well, your original integral is an 'incomplete beta function' if that's what your are after.

yea i figured that after awhile. anyway thanks a lot for your help