MathewsMD
- 430
- 7
There are two problems I am facing, and in each one, they are introducing new terms in the integration but I don't understand how.
Problem #1
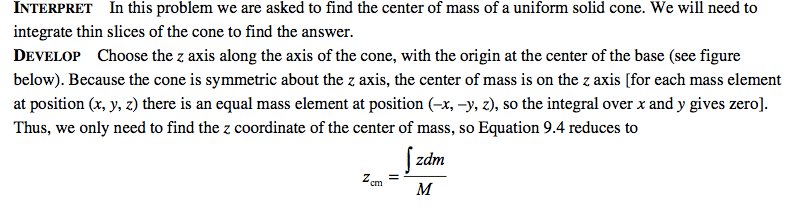

Where I become lost is r=R(1-z/h)
Why is this not just r=R(z/h)? Where does the 1-z come from?
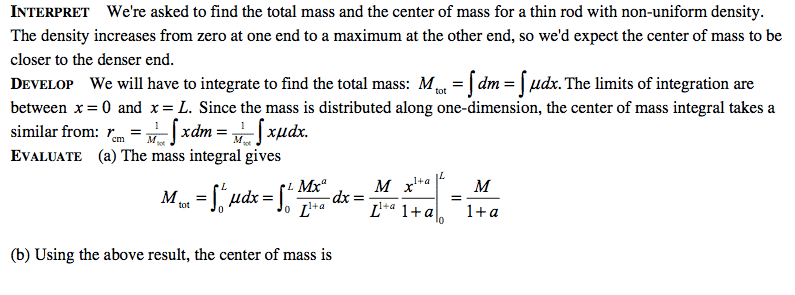
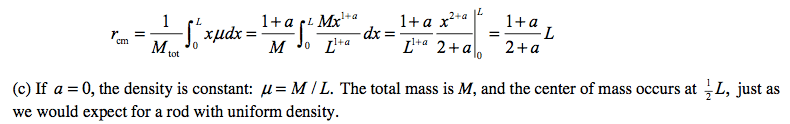
In this question, there is an integration for part b. Where I become confused is when they pull 1+a out of the integral. Where does this 1+a come from? I am relatively new to integration but know the basics. I guess I just can't seem to reason why some of these steps are being done.
Any guidance would be great! :)
Problem #1
Where I become lost is r=R(1-z/h)
Why is this not just r=R(z/h)? Where does the 1-z come from?
In this question, there is an integration for part b. Where I become confused is when they pull 1+a out of the integral. Where does this 1+a come from? I am relatively new to integration but know the basics. I guess I just can't seem to reason why some of these steps are being done.
Any guidance would be great! :)