user3
- 59
- 0
Hello,
In my textbook(Serway), Constructive interference of two rays hitting the first and the second planes , respectively, of a crystal lattice is derived as 2dsin(Θ)=mλ , where Θ is the angle shown in the picture.
My question is: shouldn't the equation be 2dsin(Θ) = (m+1/2 )λ instead? because the salt crystal is a "heavier" (larger refractive index) medium than air, so the first ray exhibits a 180 degrees phase shift.
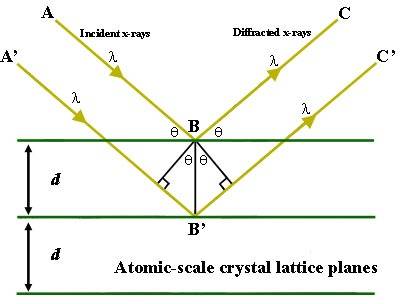
In my textbook(Serway), Constructive interference of two rays hitting the first and the second planes , respectively, of a crystal lattice is derived as 2dsin(Θ)=mλ , where Θ is the angle shown in the picture.
My question is: shouldn't the equation be 2dsin(Θ) = (m+1/2 )λ instead? because the salt crystal is a "heavier" (larger refractive index) medium than air, so the first ray exhibits a 180 degrees phase shift.